Question

If \[x=2\left( \cos \text{t}-\sin \text{t} \right)\]; \[y=3\left( \cos \text{t}+\sin \text{t} \right)\] represents a conic, its foci are:
a)\[(\pm \sqrt{10},0)\]
b)\[(\pm \sqrt{13},0)\]
c)\[(0,\pm \sqrt{13})\]
d)\[(0,\pm \sqrt{10})\]

Answer 1

Hint: Firstly, try to find the conic represented by the given function by simplifying the equations using mathematical identities and get an equation in terms of x and y.
Then convert the equations into a standard form of any conic section (i.e. ellipse, parabola, or hyperbola).
Circle: $ {{\left( x-h \right)}^{2}}+{{\left( y-k \right)}^{2}}={{r}^{2}} $
Parabola: \[\left\{ \begin{align}
  & y=\dfrac{{{\left( x-h \right)}^{2}}}{4a}+k \\
 & x=\dfrac{{{\left( y-k \right)}^{2}}}{4a}+h \\
\end{align} \right\}\]
Ellipse: \[\dfrac{{{\left( x-h \right)}^{2}}}{{{a}^{2}}}+\dfrac{{{\left( y-k \right)}^{2}}}{{{b}^{2}}}=1\]
Hyperbola: \[\left\{ \begin{align}
  & \text{for a b : }\dfrac{{{\left( x-h \right)}^{2}}}{{{a}^{2}}}-\dfrac{{{\left( y-k \right)}^{2}}}{{{b}^{2}}}=1 \\
 & \text{for a b : }\dfrac{{{\left( y-k \right)}^{2}}}{{{b}^{2}}}-\dfrac{{{\left( x-h \right)}^{2}}}{{{a}^{2}}}=1 \\
\end{align} \right\}\]\[\left\{ \begin{align}
  & \text{for a b : }\dfrac{{{\left( x-h \right)}^{2}}}{{{a}^{2}}}-\dfrac{{{\left( y-k \right)}^{2}}}{{{b}^{2}}}=1 \\
 & \text{for a b : }\dfrac{{{\left( y-k \right)}^{2}}}{{{b}^{2}}}-\dfrac{{{\left( x-h \right)}^{2}}}{{{a}^{2}}}=1 \\
\end{align} \right\}\]
After getting the equation of the conic section, find the foci for the required conic section.

Complete step-by-step answer:
Consider the given functions:
\[\begin{align}
  & x=2\left( \cos \text{t}-\sin \text{t} \right)......(1) \\
 & y=3\left( \cos \text{t}+\sin \text{t} \right)......(2) \\
\end{align}\]
Squaring the both sides of equation (1) & (2),
By applying the identities:\[\left[ \begin{align}
  & \because {{\left( a+b \right)}^{2}}={{a}^{2}}+{{b}^{2}}+2ab \\
 & \because {{\left( a-b \right)}^{2}}={{a}^{2}}+{{b}^{2}}-2ab \\
\end{align} \right]\]\[\left[ \begin{align}
  & \because {{\left( a+b \right)}^{2}}={{a}^{2}}+{{b}^{2}}+2ab \\
 & \because {{\left( a-b \right)}^{2}}={{a}^{2}}+{{b}^{2}}-2ab \\
\end{align} \right]\]
we get:
 \[\begin{align}
  & {{x}^{2}}=4\left( {{\cos }^{2}}\text{t +}{{\sin }^{2}}\text{t}-2\sin \text{t}\text{.}\cos \text{t} \right)......(3) \\
 & {{y}^{2}}=9\left( {{\cos }^{2}}\text{t}+{{\sin }^{2}}\text{t }+\text{ }2\sin \text{t}\text{.}\cos \text{t} \right)......(4) \\
\end{align}\]

We can also write above equations as:
\[\begin{align}
  & \dfrac{{{x}^{2}}}{4}=\left( {{\cos }^{2}}\text{t +}{{\sin }^{2}}\text{t}-2\sin \text{t}\text{.}\cos \text{t} \right)......(5) \\
 & \dfrac{{{y}^{2}}}{9}=\left( {{\cos }^{2}}\text{t}+{{\sin }^{2}}\text{t }+\text{ }2\sin \text{t}\text{.}\cos \text{t} \right)......(4) \\
\end{align}\]
Add both the equations (5) & (6), we get:
\[\begin{align}
  & \dfrac{{{x}^{2}}}{4}+\dfrac{{{y}^{2}}}{9}=\left( {{\cos }^{2}}\text{t +}{{\sin }^{2}}\text{t}-2\sin \text{t}\text{.}\cos \text{t} \right) \\
 & +\left( {{\cos }^{2}}\text{t}+{{\sin }^{2}}\text{t }+\text{ }2\sin \text{t}\text{.}\cos \text{t} \right) \\
 & ={{\left( {{\cos }^{2}}\text{t +}{{\sin }^{2}}\text{t} \right)}^{2}}.......(7)
\end{align}\]
Since \[\left( {{\cos }^{2}}\text{t +}{{\sin }^{2}}\text{t} \right)=1\], equation (7) becomes:
\[\dfrac{{{x}^{2}}}{4}+\dfrac{{{y}^{2}}}{9}=2......(8)\]
Equation (8) can also be written as: \[\dfrac{{{x}^{2}}}{8}+\dfrac{{{y}^{2}}}{18}=1......(9)\]

Compare equation (8) with the standard form of various conic sections.
We get to know that equation (8) represents ellipse whose standard form of equation is \[\dfrac{{{\left( x-h \right)}^{2}}}{{{a}^{2}}}+\dfrac{{{\left( y-k \right)}^{2}}}{{{b}^{2}}}=1\]
Hence, \[\dfrac{{{x}^{2}}}{8}+\dfrac{{{y}^{2}}}{18}=1\] is an ellipse, where h=k=0; a= $ \sqrt{8} $ and b= $ \sqrt{18} $ .
Since a < b, the major axis of ellipse is parallel to the y-axis.
The ellipse represented by equation (8) is shown with the help of a diagram below. Here BD is the major axis and AC is the minor axis.
The foci of the ellipse lies on the major axis which is the y-axis itself. Those are represented by E $ \left( 0,be \right) $ and F $ \left( 0,-be \right) $ where ‘e’ is the eccentricity of the ellipse.

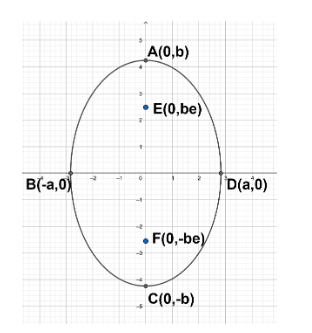
Now to find the foci of the ellipse, we need to calculate the eccentricity (e) of the ellipse.
i.e. for ellipse \[\dfrac{{{\left( x-h \right)}^{2}}}{{{a}^{2}}}+\dfrac{{{\left( y-k \right)}^{2}}}{{{b}^{2}}}=1\];
If a < b, then $ e=\sqrt{1-\dfrac{{{b}^{2}}}{{{a}^{2}}}} $ $ e=\sqrt{1-\dfrac{{{a}^{2}}}{{{b}^{2}}}} $
If a > b, then $ e=\sqrt{1-\dfrac{{{b}^{2}}}{{{a}^{2}}}} $
Therefore, eccentricity of the given ellipse \[\dfrac{{{x}^{2}}}{8}+\dfrac{{{y}^{2}}}{18}=1\] is \[e=\sqrt{1-\dfrac{8}{18}}\]
 \[e=\sqrt{\dfrac{10}{18}}\]
\[e=\sqrt{\dfrac{2\times 5}{2\times 9}}\]
\[e=\dfrac{\sqrt{5}}{3}\]
So focii of given ellipse are \[\left( 0,\sqrt{18}\times \dfrac{\sqrt{5}}{3} \right)\] and \[\left( 0,-\sqrt{18}\times \dfrac{\sqrt{5}}{3} \right)\]
i.e. \[(0,+\sqrt{10})\]and \[(0,-\sqrt{10})\]
So, the correct answer is “Option D”.

Note: Be careful while identifying the major axis of ellipse while considering the values of a and b because it might change the value of eccentricity and therefore foci would lie parallel to the x-axis in another case (i.e. a > b).
Suppose we subtract the square of both the equations instead of adding them to simplify and get an equation in terms of x and y.