Question

In a circle of diameter 10cm, the length of each of 2 equal and parallel chords is 8cm, find the distance between these two chords.
A. 4cm
B. 5cm
C. 6cm
D. 7cm

Answer 1

Hint-Using the data given, first construct a figure, and apply Pythagoras theorem for the triangles formed and solve this question.

Complete step-by-step answer:

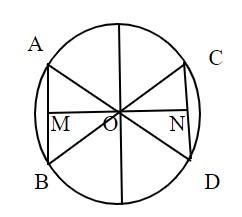
In the figure, let us consider AB and CD are the two chords of length 8cm respectively
Now, let us draw a perpendicular OM to AB and ON to CD and we know that a perpendicular drawn from the centre to the chord bisects the chord
So, from this we can write CN=ND=4cm, and AM=MB=4cm,
 OM=radius of the circle=$\dfrac{{diameter}}{2}$ =$\dfrac{{10}}{2} = 5cm$
Now, let us apply Pythagoras theorem in triangle AOM and CON
So ,in triangle AOM, we get
$
  O{A^2} = A{M^2} + O{M^2} \\
  {5^2} = O{M^2} + {4^2} \\
   \Rightarrow OM = \sqrt {25 - 16} = \sqrt 9 = 3 \\
 $
In triangle CON, we get
$
  O{C^2} = N{C^2} + O{N^2} \\
  {5^2} = O{N^2} + {4^2} \\
   \Rightarrow ON = \sqrt {25 - 16} = \sqrt 9 = 3 \\
 $
But , in the question we had to find out the distance between the two chords, which is nothing but the length of MN
But MN=OM+ON
MN=3+3=6cm
So, from this, we get the perpendicular distance between the two chords is 6cm
Note: When solving these type of questions, if the diameter is given, first find out the radius from this and then use it in the formula and solve it and also make use of the Pythagoras theorem and find out the length of the required quantity.