Question

In a class, 62 students speak assamese, 25 speak hindi and 1 student speak both the languages. How many speak at least one of these languages?

Answer 1

Hint: We have to find the number of students who speak either Assamese or hindi or both. We will use formula $A \cup B = A + B - A \cap B$

Complete step-by-step answer:
First of all, let us see what is given to us.
Let n(h) be the number of students who speak hindi language, n(a) be the number of students who speak Assamese language. Therefore, the number of students who speak both Hindi and Assamese is represented by $n(a \cap h)$ which means the intersection of both the languages.
We can use the Venn diagram to represent the solution and concept.

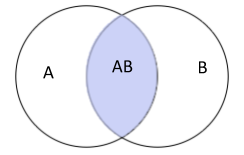
In the above diagram, A represents the n(a) and B represent the n(h). A $ \cap $B represent n(a$ \cap $b) and hence A $ \cup $B is given by
$
   \Rightarrow A \cup B = A + B - A \cap B \\
   \Rightarrow n(a \cup h) = n(a) + n(h) - n(a - h) \\
   \Rightarrow n(a \cup b) = 25 + 62 - 1 \\
   \Rightarrow n(a \cup b) = 86 \\
$
Here, n$(a \cup b)$represents the number of students who speak Assamese or students who speak Hindi or students who speak both the languages. So, 86 students speak at least one of these languages.
So, the total number of students who speak at least one of these languages is 86.

Note: Now if we solve this by mind, how we can calculate it directly. We will see how many students speak assamese language, there are 62 students speaking assamese and this also includes who speaks hindi and assamese both i.e. 1 student. So, the number of students who speak only Assamese is 61. After this, we will see how many students speak hindi language, there are 25 students speaking hindi and this also includes who speaks hindi and assamese both i.e. 1 student. So, the number of students who speak only hindi is 24. For finding the number of students who speak at least one of these languages is obtained by adding the number of students who speak hindi, assamese and both the languages i.e. \[61 + 24 + 1 = 86\]. Most common mistakes done by students are not considering the case of who speaks both the languages as they give at least one of these languages which is wrong.