Question

In a closed organ pipe of 105cm, standing waves are set up corresponding to the third overtone. At what distance from the closed end, a pressure node is formed?
A.) 5 cm
B.) 45 cm
C.) 25 cm
D.) 30 cm

Answer 1

Hint: Organ pipes are open at one end and closed at the other. The antinodes are formed at the open end and nodes form at the closed end. Pressure Nodes occur at point where the displacements form antinodes.

Formula used: ${n^{th}}$ harmonic of an open pipe of length $L$ follows the relation : $L = \left( {2n - 1} \right)\dfrac{\lambda }{4}$

Complete Step by Step answer:
When reflected waves from one end superpose with the initial incident waves, the resulting wave pattern is called a standing wave.

The figure fig(2) shows such a pattern for the case of a one-side open pipe (as in case of an organ pipe) of length $L$

The particles at the open end of the pipe are oscillating back and forth and hence form an antinode whereas those at the closed are not moving and form a node.

The different possible wavelengths of sound that can form such a standing wave inside this given pipe are shown in fig(2).

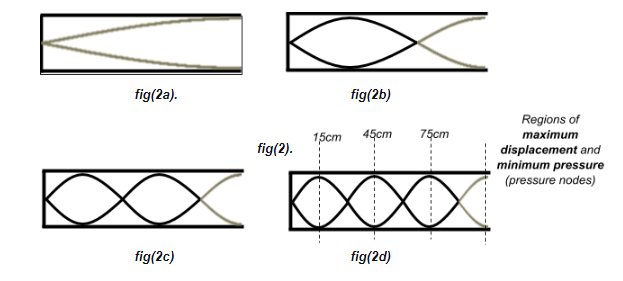
fig(2a) corresponds to the fundamental frequency, fig(2b) is the second harmonic, which is also called the first overtone. fig(2c) is the third harmonic or the second overtone and so on.

Here since the sound has produced a third overtone in the pipe. It corresponds to fig(2d). Now we can relate the length of the pipe and the wavelength of sound as:

$L = \left( {3\dfrac{\lambda }{2} + \dfrac{\lambda }{4}} \right) = 7\dfrac{\lambda }{4}$

Now, we are asked where the pressure node would be. Since the particles are stationary at the nodes, they get compressed closer together. Thus, the pressure would be high at nodes and minimum at antinodes. So the pressure nodes occur at points where displacement is maximum and vice versa.

From equation , we can find the wavelength of standing wave:

$7\dfrac{\lambda }{4} = 105$
$\dfrac{\lambda }{4} = 15$
$\lambda = 60cm$

Now, we see from the figure that the distance to the nearest antinode, which would also be the pressure node is $\dfrac{\lambda }{4} = 15cm$. The next pressure node would be at $45cm$ and the next at $75cm$.

Thus, we see that option B is a possible pressure node and hence the answer.

Note: A common possible mistake could be to consider displacement nodes as pressure nodes and mark option D as correct. We must be careful and expect such one-word traps in the question.