Question

In a conference $10$ speakers are present. If ${{\text{S}}_1}$ wants to before ${{\text{S}}_2}$ and ${{\text{S}}_2}$ wants to speak after ${{\text{S}}_3}$, then the number of ways all the $10$ speakers can give their speeches with the above restriction if the remaining seven speakers have no objection to speak at any number is,
$
  ({\text{A}})\,{}^{10}{{\text{C}}_3} \\
  ({\text{B}})\,{}^{10}{{\text{P}}_8} \\
  ({\text{C}})\,{}^{10}{{\text{P}}_3} \\
  ({\text{D}})\,\dfrac{{10!}}{3} \\
 $

Answer 1

Hint:
The question is based on permutation and combination. In the given there are ten speakers, out of those three speakers have the order to speak. Then the remaining seven speakers have no order to speak. We have to find the number of ways all the speakers can give their speech.

Useful formula:
The formulae used in this question are,
The permutation formula is,
 ${}^{\text{n}}{{\text{P}}_{\text{r}}} = \dfrac{{{\text{n!}}}}{{({\text{n}} - {\text{r}})!}}$
 ${\text{n}}$ be the total number of objects
 ${\text{r}}$ be the number of objects used to form the permutation

Complete step by step solution:
The data given in the question are,
The total number of speakers is $10$
The number of speakers have the order to speak is $3$

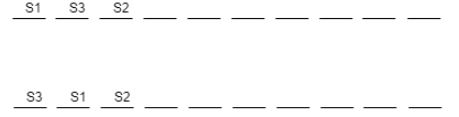
From the diagram above we can say that seven speakers don’t have any order to speak.
Substitute the values in the permutation formula we get,
 $ \Rightarrow \dfrac{{{\text{10!}}}}{{(10 - 3)!}}$
The above equation will be equal to,
 $ \Rightarrow {}^{10}{{\text{P}}_3}$
 $\therefore $ the required value will be ${}^{10}{{\text{P}}_3}$ .
Hence, the number of ways all the $10$ speakers can give their speeches with the above restriction is ${}^{10}{{\text{P}}_3}$ ways.

Thus, the option $({\text{C}})$ is correct.

Note:
The main difference between permutation and combination is that, in permutation the order of arrangement matters but in combination the order of arrangement does not matter. The permutation is an example to the password, if some changes occur or if order changes then it is invalid. Thus order matters in permutation.