Question

In a $\Delta ABC$, right angled at B, the in –radius is:
A. $\dfrac{AB+BC-AC}{2}$
B. $\dfrac{AB+AC-BC}{2}$
C. $\dfrac{AB+BC+AC}{2}$
D. None

Answer 1

Hint: The radius of a triangle is equal to $\dfrac{\Delta }{s}$. Where $'\Delta '$ is the area of the triangle and ‘s’ is the semi- perimeter of the triangle. We can find the area by taking the product of base and height and then dividing it by 2. We can find the semi-perimeter by adding up all the side lengths and then dividing it by 2. Find $'\Delta '$ and ‘s’ of triangles and put in the formula to get the inradius.

Complete step-by-step answer:
Given triangle ABC is right angled at B.

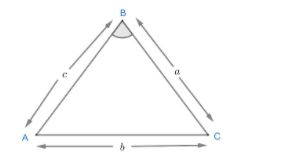
\[\begin{align}
  & Area\ of\ a\ triangle\ is\ =\dfrac{1}{2}\times \left( base \right)\times \left( height \right) \\
 & \Rightarrow \Delta =\dfrac{1}{2}\times \left( AB \right)\times \left( BC \right) \\
 & Semiperimeter\ of\ \Delta ABC=\dfrac{Perimeter\ of\ \Delta ABC}{2} \\
 & \Rightarrow s=\dfrac{AB+BC+AC}{2} \\
 & \Rightarrow s=\dfrac{a+b+c}{2}.......\left( 1 \right) \\
\end{align}\]
Now, let us put calculated values of $'\Delta '$ and ‘s’ in the formula of inradius;
$\begin{align}
  & r=\dfrac{\Delta }{s} \\
 & \Rightarrow r=\dfrac{\left( \dfrac{1}{2}\times AB\times BC \right)}{\left( \dfrac{AB+BC+CA}{2} \right)} \\
\end{align}$
Multiplying both numerator and denominator by 2, we will get,
$\Rightarrow r=\dfrac{AB\times BC}{AB+BC+AC}$
Putting AB = c, BC = a and AC = b, we will get;
$\begin{align}
  & \Rightarrow r=\dfrac{c\times a}{c+a+b} \\
 & \Rightarrow r=\dfrac{ac}{a+b+c}...........\left( 2 \right) \\
\end{align}$
Subtracting equation (1) from equation (2), we will get,
$\Rightarrow r-s=\dfrac{ac}{a+b+c}-\dfrac{a+b+c}{2}$
Taking LCM and subtracting, we will get,
$\Rightarrow r-s=\dfrac{2ac-{{\left( a+b+c \right)}^{2}}}{2\left( a+b+c \right)}$
 We know ${{\left( a+b+c \right)}^{2}}={{a}^{2}}+{{b}^{2}}+{{c}^{2}}+2ab+2bc+2ca$.
Using these identity, we will get,
$\begin{align}
  & \Rightarrow r-s=\dfrac{2ac-\left( {{a}^{2}}+{{b}^{2}}+{{c}^{2}}+2ab+2bc+2ca \right)}{2\left( a+b+c \right)} \\
 & \Rightarrow r-s=\dfrac{{2ac}-{{a}^{2}}-{{b}^{2}}-{{c}^{2}}-2ab-2bc-{2ca}}{2\left( a+b+c \right)} \\
\end{align}$
Taking “-1” common, we will get,
$\Rightarrow r-s=\dfrac{-\left( {{a}^{2}}+{{b}^{2}}+{{c}^{2}}+2ab+2bc \right)}{2\left( a+b+c \right)}$
As $\Delta ABC$ is right angled at B,
 $\begin{align}
  & {{\left( hypotenuse \right)}^{2}}={{\left( side\ 1 \right)}^{2}}+{{\left( side\ 2 \right)}^{2}} \\
 & \Rightarrow {{b}^{2}}={{a}^{2}}+{{c}^{2}} \\
\end{align}$
By replacing ${{a}^{2}}+{{c}^{2}}$with ${{b}^{2}}$, we will get,
$\Rightarrow r-s=\dfrac{-\left( {{b}^{2}}+{{b}^{2}}+2ab+2bc \right)}{2\left( a+b+c \right)}$
Multiplying both sides of equation by “-1”, we will get,
$\begin{align}
  & \Rightarrow -1\times \left( r-s \right)=\left( -1 \right)\times \left[ \dfrac{-\left( 2{{b}^{2}}+2ab+2bc \right)}{2\left( a+b+c \right)} \right] \\
 & \Rightarrow s-r=\dfrac{2{{b}^{2}}+2ab+2bc}{2\left( a+b+c \right)} \\
\end{align}$
Taking “2b” common from the numerator in RHS, we will get,
\[\Rightarrow s-r=\dfrac{2b\left( b+a+c \right)}{2\left( a+b+c \right)}\]
Dividing both numerator and denominator by 2(a + b + c), we will get,
$\begin{align}
  & \Rightarrow s-r=b \\
 & \Rightarrow r=s-b \\
\end{align}$
Putting $s=\dfrac{a+b+c}{2}$, we will get,
$r=\left( \dfrac{a+b+c}{2} \right)-\dfrac{b}{1}$
Taking LCM and subtracting, we will get,
$\begin{align}
  & r=\dfrac{a+b+c-2b}{2} \\
 & \Rightarrow r=\dfrac{a-b+c}{2} \\
\end{align}$
Now, putting a = BC, b = AC, c = AB, we will get,
$\begin{align}
  & \Rightarrow r=\dfrac{BC-AC+AB}{2} \\
 & \Rightarrow r=\dfrac{AB+BC-AC}{2} \\
\end{align}$
Hence, the inradius of $\Delta ABC$ is equal to $\dfrac{AB+BC-AC}{2}$ and option (A) is the correct answer.

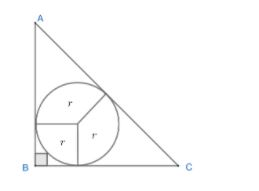
Note: inradius of a triangle is the radius of the circle inscribed in the triangle. If you don’t remember the formula for inradius. Calculate inradius using geometry. But this will be a very lengthy method, so try to memorize the formula.