Question

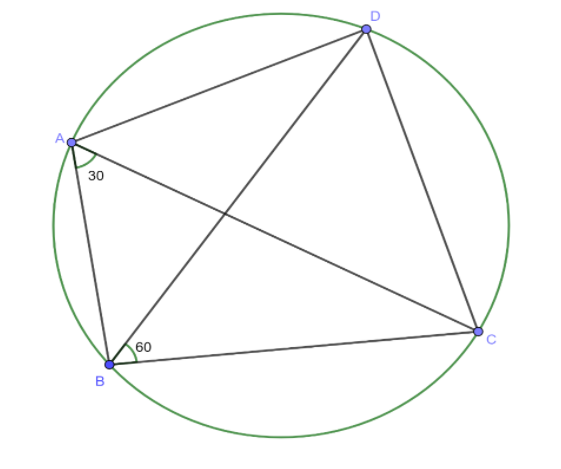
In a given figure, ABCD is a cyclic quadrilateral, in which AC and BD are its diagonal. If \[\angle DBC = {60^ \circ }\] and \[\angle BAC = {30^ \circ }\], the find \[\angle BCD\]

Answer 1

Hint: Here in this question we have to determine the value of \[\angle BCD\]. The given diagram is a cyclic quadrilateral. First we use one of the theorems of cyclic quadrilateral i.e., angles in the same segment are equal, we determine the value of \[\angle CAD\]. On adding the angles \[\angle CAD\] and \[\angle BAC\], find the value of \[\angle BAD\]. Then by considering the another theorem of cyclic quadrilateral i.e., the sum of either pair of opposite angles of a cyclic quadrilateral is \[{180^ \circ }\], we are going to determine the value of \[\angle BCD\].

Complete step-by-step answer:
A cyclic quadrilateral is a quadrilateral which has all its four vertices lying on a circle. It is also sometimes called inscribed quadrilateral. The circle which consists of all the vertices of any polygon on its circumference is known as the circumcircle or circumscribed circle.
Now we consider the given question
The points A and B on this circle subtend angles \[\angle DBC\] and \[\angle CAD = {60^ \circ }\]. Because these angles lie in the same segment.
Therefore the \[\angle BAD = \angle BAC + \angle CAD\]
On substituting the values we have
\[ \Rightarrow \angle BAD = {30^ \circ } + {60^ \circ }\]
On adding we have
\[ \Rightarrow \angle BAD = {90^ \circ }\]
By the theorem of cyclic quadrilateral we know that the sum of either pair of opposite angles of a cyclic quadrilateral is \[{180^ \circ }\]
Therefore we have
\[ \Rightarrow \angle BAD + \angle BCD = {180^ \circ }\]
On substituting the value of \[\angle BAD = {90^ \circ }\]we have
\[ \Rightarrow {90^ \circ } + \angle BCD = {180^ \circ }\]
Take \[{90^ \circ }\] to RHS we have
\[ \Rightarrow \angle BCD = {180^ \circ } - {90^ \circ }\]
On simplifying we have
\[ \Rightarrow \angle BCD = {90^ \circ }\]
Therefore the value of \[\angle BCD = {90^ \circ }\]
So, the correct answer is “ \[\angle BCD = {90^ \circ }\]”.

Note: Especially in finding the angles of some mathematical figures we have to know the theorems which are related to that figure. The quadrilateral is different from the cyclic quadrilateral. We have to remember the theorems which is related to the cyclic quadrilateral is given below:
1. In a cyclic quadrilateral, the sum of either pair of opposite angles is supplementary.
2. The ratio between the diagonals and the sides can be defined and is known as the Cyclic quadrilateral theorem. If there’s a quadrilateral which is inscribed in a circle, then the product of the diagonals is equal to the sum of the product of its two pairs of opposite sides.
3. Angles in the same segment are equal.