Question

In a hostel 60% had vegetarian lunch while 30% had non-vegetarian lunch and 15% had both types of lunch. If 96 people were present how many did not eat either type of lunch?
A. \[20\]
B. \[24\]
C. \[26\]
D. \[28\]

Answer 1

Hint: We can solve this question with the help of Venn diagram. We will substitute the values of percentage of people eating vegetarian, non-vegetarian and both types of food in the formula for union to find total percentage of people eating food and then we subtract it from total number of people present there.

Complete step-by-step answer:
Draw the Venn diagram for this question by denoting people choosing vegetarian food by V and non-vegetarian by N and people choosing both by V&N.

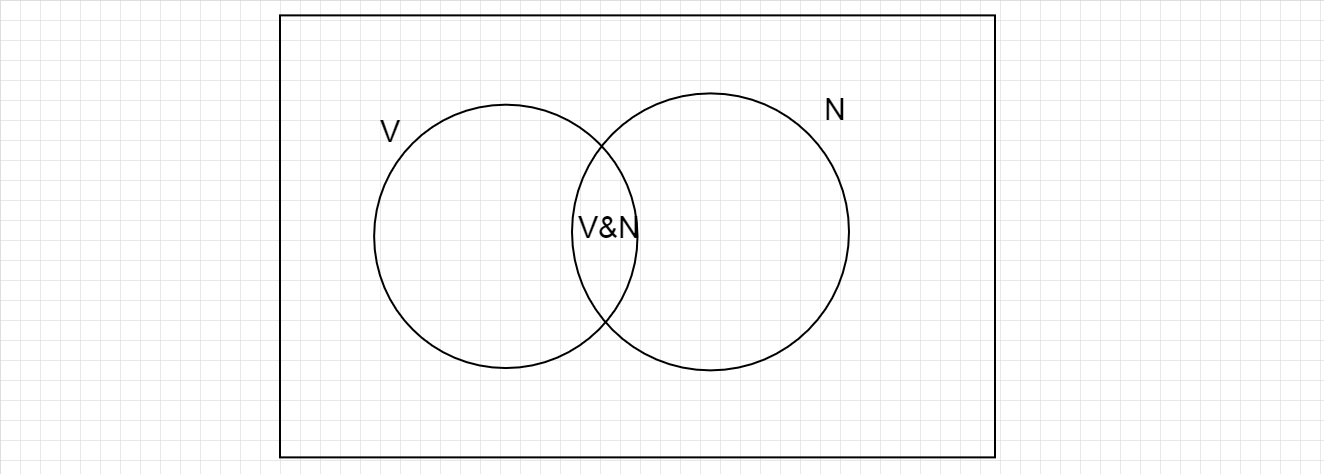
Then, we can write
Percentage of people having vegetarian lunch as \[n(V) = 60\]
Percentage of people having non-vegetarian lunch as \[n(N) = 30\]
Percentage of people having both vegetarian and non-vegetarian lunch as \[n(V \cap N) = 15\]
Using the formula of union we can find number of people having lunch i.e. \[n(V \cup N)\]
Since, \[n(A \cup B) = n(A) + n(B) - n(A \cap B)\]
Substitute \[A = V,B = N\]
\[n(V \cup N) = n(V) + n(N) - n(V \cap N)\]
Substituting the values of \[n(V) = 60\], \[n(N) = 30\] and \[n(V \cap N) = 15\].
\[n(V \cup N) = 60 + 30 - 15\]
                    \[ = 90 - 15 = 75\]
Therefore, \[75\% \] people having lunch.
Now to find number of people not having either type of lunch we subtract percentage of people having lunch from total percentage i.e. \[100\% \]
\[100\% - 75\% = 25\% \]
Therefore, \[25\% \] people are not having any type of lunch.
Now we calculate the value of \[25\% \] of number of people present there i.e. \[96\]
Since, we know to find percentage \[x\% \] of a number \[m\] we use the formula \[\dfrac{x}{{100}} \times m\]
Therefore, \[25\% \] of \[96\] people \[ = \dfrac{{25}}{{100}} \times 96\]
                                                          \[ = \dfrac{{25}}{{25 \times 4}} \times 96\]
                                                          \[ = \dfrac{{96}}{4}\] { cancel out same terms from numerator and denominator}
                                                          \[ = 24\]

Therefore, option B is correct.

Note:
Students are likely to get confused in these types of questions and they end up solving for the number of people having lunch instead of finding the number of people not having any type of lunch because there we need to subtract from the total the number of people having lunch. Students should draw the Venn diagram for better understanding of the concept. Since, this question was given in terms of percentage, students should try to solve most of the part in terms of percentage and in the end find the value of percentage.