Question

In a Lloyd’s mirror experiment, a light wave emitted directly from the source $S$ interferes with the reflected light from the mirror. The screen is $1m$ away from the source $S$. The size of the fringe width is $0.25mm$. The source is moved $0.6mm$ above the initial position, the fringe width decreases by $1.5$ times. If the light wave used is in the wavelength $2.4\times {{10}^{-x}}$, find the value of $x$.

Answer 1

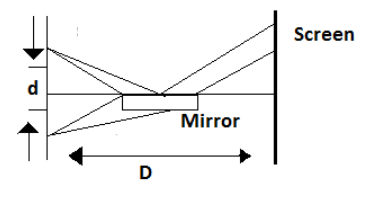
Hint: We know that Lloyd’s mirror experiment tells us about the fact that light from the monochromatic slit source reflects from a glass surface at a small angle and appears to come from a virtual source as a result. The reflected light interferes with the direct light from the source, forming interference fringes. The interference pattern in this experiment is different from that of Young’s experiment.
Formula Used: We will use the following relation to solve the given problem:-
$\beta =\dfrac{D\lambda }{d}$.

Complete answer:
From the question above we have the following parameters with us:-
Distance between screen and source,$D=1m$
Size of fringe width, $\beta =0.25mm=0.25\times {{10}^{-3}}m$
Distance between the slits is $d$.
Wavelength, $\lambda =2.4\times {{10}^{-x}}$, we have to find the value of $x$.
In Lloyd experiment we have

$\beta =\dfrac{D\lambda }{d}$……………….. $(i)$
Putting the given values in $(i)$ we get
$0.25\times {{10}^{-3}}=\dfrac{D\lambda }{d}$
$0.25\times {{10}^{-3}}\times d=D\lambda $
$\lambda =\dfrac{d\times {{10}^{-3}}}{4}$……………… $(ii)$
Now the source is moved by $0.6mm$. The net movement will be $1.2mm$ as the image will also move by that much margin.
So the second case is as follows:-
Total shift will be$d+1.2\times {{10}^{-3}}$.
Hence, equation for $\beta $will be as follows
$\beta =\dfrac{D\lambda }{d+1.2\times {{10}^{-3}}}$
$\lambda =\dfrac{0.25\times {{10}^{-3}}d}{1.5}=\dfrac{{{10}^{-3}}d}{6}$…………….$(iii)$
This can also be written as
$\lambda D=\dfrac{{{10}^{-3}}d}{6}+\dfrac{1.2\times {{10}^{-3}}\times {{10}^{-3}}}{6}$
Using $(i)$we get
$\Rightarrow \lambda =\dfrac{d\times {{10}^{-3}}}{4D}$
$\Rightarrow \lambda =\dfrac{0.6\times {{10}^{-3}}\times {{10}^{-3}}}{1}$ (Putting,$D=1m$)
$\Rightarrow \lambda =0.6\times {{10}^{-6}}m$
$\Rightarrow \lambda =0.6\mu m$…………………. $(iv)$
From the above equations and conditions given in the problem we get
$\Rightarrow \dfrac{d}{4}=\dfrac{d}{6}+\dfrac{1.2\times {{10}^{-3}}}{6}$
$\Rightarrow d=2.4\times {{10}^{-3}}m$.
According to the condition given in the problem we have $d=\lambda $.
Comparing this with the value of $\lambda =2.4\times {{10}^{-x}}$ given in the problem we get $x=3$.

Note:
We have to consider the fact that Lloyd’s mirror experiment has the same geometry as the double slit experiment except that one light source is the image of the other one. In solving problems of Lloyd’s mirror experiment we should be also careful of the fact that there is a phase shift of $\pi $ for the reflected light. Light is always taken as monochromatic in Lloyd’s mirror experiment.