Question

In a parallelogram ABCD, angle $\angle DAB=40^{\circ}$. then find the other angles of the parallelogram.

Answer 1

Hint: In this question, one angle of the parallelogram is given and we need to find the other three angles. We also know that a parallelogram is a quadrilateral in which each pair of opposite sides is parallel. By using the properties of the parallelogram we can find the other three angles of the parallelogram.

Complete step-by-step solution:

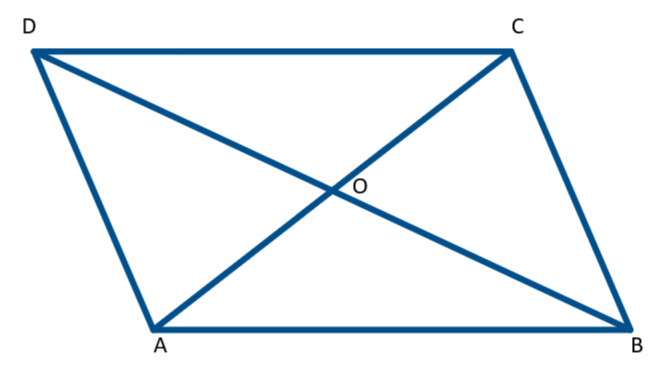
Given, \[{ABCD}\] is a parallelogram
And \[\angle DAB\ = \ 40^{\circ}\]
We know that in a parallelogram, opposite sides are parallel.
i.e). \[AD\ \parallel \ BC\]
By this we can conclude that
\[\angle DAB\ = \ \ \angle BCD\ = \ 40^{\circ}\]
Thus we have found one angle \[\angle BCD\ = \ 40^{\circ}\]
We also know that the sum of consecutive angles are \[180^{\circ}\]
The consecutive angles in the parallelogram are \[\angle CBA\] and \[\angle DAB\]
\[\angle CBA\ + \ \angle DAB\ = \ 180^{\circ}\]
We have already found the value of \[\angle DAB\ = \ 40^{\circ}\]
By substituting the know value,
We get,
 \[\angle CBA\ + \ 40^{\circ}\ = \ 180^{\circ}\]
\[\ \angle CBA\ = \ 180^{\circ} - \ 40^{\circ}\]
By subtracting,
We get,
\[\angle CBA\ = \ 140^{\circ}\]
Again by using the concept that in parallelogram opposite sides are parallel.
 \[\angle ADC\ = \ \ \angle CBA\ = \ 140^{\circ}\]
Thus the other angles of the parallelogram are \[40^{\circ}\] , \[140^{\circ}\] and \[140^{\circ}\]
Final answer :
The other angles of the parallelogram are \[40^{\circ}\] , \[140^{\circ}\] and \[140^{\circ}\]

Note: The properties of the parallelogram are opposite sides of the parallelogram are equal and the opposite angles of the parallelogram are also equal. There are \[4\] edges in the parallelogram. The area of the parallelogram is the product of base and height
\[Area\ = \ b \times h\]