Question

In a practical Wheatstone bridge circuit, wire AB is 2 m long. When resistance Y=2.0 W and jockey is in position J such that AJ=1.20 m, there is no current in the galvanometer, find the value of unknown resistance X. The resistance per unit length of wire AB=0.01 W/cm. Also calculate the current drawn by the cell of emf 4.0 V and negligible internal resistance.

Answer 1

Hint: Wheatstone bridge is an experimental setup which is used to measure an unknown resistance. It has four arms which act as resistors, and the ratio of two of the resistors is kept fixed. From balancing the other two arms of the bridge we can calculate the unknown resistance. We will be using a suitable formula in relation to wheatstone bridge to find the unknown resistance and the current drawn from the battery.

Complete Step-By-Step answer:
We have been given that,
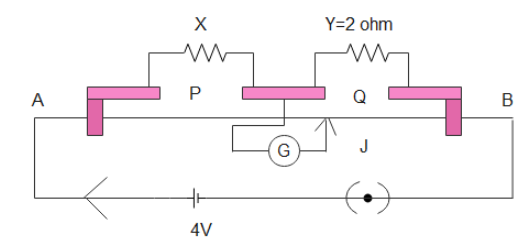
AB=2m
Y= 2 \[\Omega \]
AJ = 1.20m
Emf = 4V
The Resistance offered by wire AB = 0.01\[\Omega \]/cm

We will start by looking into the diagram,
We can see that,
P = Resistance of wire AJ
\[\begin{align}
  & P=(1.20\times 100cm)\times (0.01\Omega /cm) \\
 & P=1.20\Omega \\
\end{align}\]
Q= Resistance of wire BJ
\[\begin{align}
  & Q=\left[ (2-1.20)\times 100 \right]cm\times (0.01\Omega /cm) \\
 & Q=0.80\Omega \\
\end{align}\]

We have the resistances of P and Q, now using this we will have to find the unknown resistance of resistor X.

To find the resistance of X we will use the formula,
\[\dfrac{P}{Q}=\dfrac{X}{Y}\]

Now substituting the values in the equation, will give,
\[\begin{align}
  & X=Y\times \dfrac{P}{Q} \\
 & X=2\times \dfrac{1.20}{0.80} \\
 & X=3\Omega \\
\end{align}\]
Hence the resistance of the resistor X is \[3\Omega \].

Now, let us find the total resistance of X and Y when they are connected in series,
\[\begin{align}
  & {{R}_{1}}=X+Y \\
 & {{R}_{1}}=3+2 \\
 & {{R}_{1}}=5\Omega \\
\end{align}\]

Now, finding the total resistance when P and Q are connected in series(or of wire AB),
\[\begin{align}
  & {{R}_{2}}=2\times 100\times 0.01 \\
 & {{R}_{2}}=2\Omega \\
\end{align}\]

Now we will find the resistance when \[{{R}_{1}}\] and \[{{R}_{2}}\]are connected in parallel, meaning the the effective or total resistance between the terminals A and B of Wheatstone bridge will be,
\[\begin{align}
  & {{R}_{AB}}=\dfrac{{{R}_{1}}{{R}_{2}}}{{{R}_{1}}+{{R}_{2}}} \\
 & {{R}_{AB}}=\dfrac{5(2)}{5+2}=\dfrac{10}{7}\Omega \\
\end{align}\]

Now using the above values, we will find the current drawn from the battery using the formula,
\[I=\dfrac{emf}{{{R}_{AB}}}\]
\[I=\dfrac{4}{\left( \dfrac{10}{7} \right)}=2.8A\]

Hence the current drawn from the battery is 2.8A.

Note:
The Wheatstone bridge is an instrument which can give very precise values of resistances. It is used to measure stress, strain, temperature, etc., along with the help of an operational amplifier. The formula
\[\dfrac{P}{Q}=\dfrac{X}{Y}\]
It is essential and students are recommended to remember it.