Question

In a pure semiconductor, the number of conduction electrons is $6 \times {10^{19}}$ per cubic meter. How many holes are there in a sample of size $(1cm \times 1cm \times 2mm)$?

Answer 1

Hint:First we have to convert the data into cubic meters.
Then we use the concept of intrinsic semiconductor for finding the required solution.
On some simplification, we get the answer.

Formula used:
$1cm = {10^{ - 2}}meter$
$1mm = {10^{ - 3}}meter$
The number of the conduction electron $(N)$ in a sample of the volume $(V)$ is,
$N = $ volume of the sample \[ \times \] number of conduction electrons per cubic meter.
The number of electron density is $n$and the number of hole density \[p\] is equal i.e. \[n = p\].

Complete step by step answer:
In an intrinsic semiconductor how many electrons become free, the same number of holes are created.
Here the number of electron density is $n$ and the number of hole density \[p\] is equal.
We can write it as, \[n = p\]
It is given that the number of the conduction electrons in a pure semiconductor is $6 \times {10^{19}}$ per cubic meter.
We have to calculate the number of holes in a sample of size $(1cm \times 1cm \times 2mm)$.
First, we convert the given size in the cubic meter,
So we can write it as, $1cm \times 1cm \times 2mm = ({10^{ - 2}} \times {10^{ - 2}} \times 2 \times {10^{ - 3}}){m^3} = (2 \times {10^{ - 7}}){m^3}$
$\therefore $ The number of the conduction electron $(n)$ in the sample of the volume $(2 \times {10^{ - 7}}){m^3}$ is,
$n = $ volume of the sample \[ \times \] number of conduction electrons per cubic meter.
\[\therefore n = 2 \times {10^{ - 7}} \times 6 \times {10^{19}}\]
Let us multiply the terms an we get,
\[ \Rightarrow n = 12 \times {10^{12}}\]
Since the number of the hole is equal to the number of the conduction electron,
\[n = p\]
Hence, the number of the hole(\[p\]) in the sample of the volume $(2 \times {10^{ - 7}}){m^3}$ is equal to $12 \times {10^{12}}$ .
$\therefore $ The number of holes in the sample of the volume is $12 \times {10^{12}}$

Note: We take the number of electron density is $n$ and the number of hole density \[p\] is equal.
Let in a pure Silicon crystal the electron situated in the position of ‘A’ in the bond (fig-1) breaks the bond and goes to the position ‘X’.
That means a valence electron becomes a conduction electron.
In the meantime, in the position, ‘A’ there occurs a crisis of an electron, and then in the position ‘A’ there generates a positive charge according to the corresponding electron clouds.
This crisis of electrons in the bond is named Hole.

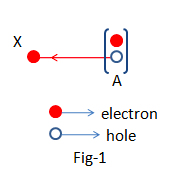
That’s why in pure semiconductor the number of electron density is $n$ and the number of hole density \[p\] is equal.