Question

In a square \[\square ABCD\], the diagonals bisect each other at point \[O\]. What type of triangle is \[\vartriangle AOB\]?
A.An equilateral triangle
B.An isosceles but not right-angled triangle
C.A right-angled but not an isosceles triangle
D.An isosceles right-angled triangle

Answer 1

Hint: In the given question, we have to identify the type of triangle formed. We can first draw the diagram and then use the properties of the triangle to arrive at the answer. The point to be noted is that, in a square, all sides are equal and diagonals bisect each other at equal length.

Complete step-by-step answer:
A square is a two-dimensional plane figure with four equal sides and four \[90\]-degree angles on all four sides. It is a regular quadrilateral. There are only two diagonals of the square and they bisect each other at right angles.
We can solve the problem as follows with the help of diagram:

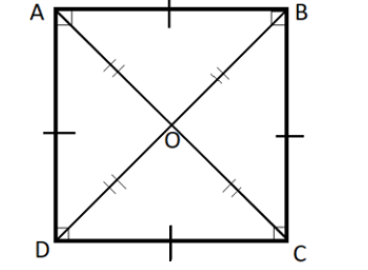
Here all the sides are equal i.e. \[AB = BC = CD = AD\] and the diagonals are equal and bisect each other at equal length i.e. \[AO = OC = OB = OD\].
Moreover, \[\angle A = \angle B = \angle C = \angle D = {90^0}\].
Since the diagonals are of equal length and bisect at \[90\]-degree angles, we can conclude that:
\[\angle OAB = \angle OBA = \angle OBC = \angle OCB = \angle OCD = \angle ODC = \angle ODA = \angle OAD = {45^0}\]
\[\angle AOB = {90^0}\] and \[OA = OB\].
Since the two sides of the triangle \[\vartriangle AOB\] are equal and one angle is right-angle we can say that it is an isosceles right-angled triangle.
Thus, Option (D) An isosceles right-angled triangle is the correct answer.
So, the correct answer is “Option D”.

Note: An isosceles triangle is one in which every two of its sides are identical. In addition, the angles on the opposite sides of these equal sides are equal. In other words, we can say that “An isosceles triangle is a triangle which has two congruent sides”.