Question

In a stationary wave, antinodes are the points where there is:
A. Minimum displacement and minimum pressure change
B. Minimum displacement and maximum pressure change
C. Maximum displacement and maximum pressure change
D. Maximum displacement and minimum pressure change

Answer 1

Hint: Recall that stationary waves are produced when two exactly identical progressive waves travel through a medium along the same path but in opposite directions and interfere with each other. This interference results in the formation of nodes and antinodes in the resultant wave.
Remember that at antinodes the amplitude of the wave is maximum, and the air flows through this region unconstrained owing to its relatively larger space (amplitude) in comparison to nodes where the air has to compress itself to get through. Using this, deduce the nature of the displacement and pressure change at antinodes.

Complete step-by-step solution:
Let us begin by understanding what stationary waves are.
Stationary waves, also known as standing waves, are formed as a result of interference of two progressive waves of the same type, same amplitude, and same frequency, traveling in opposite directions along the same line of propagation.
These waves are called stationary or standing because their individual energies get added together or get canceled out and there is no net transport of energy in the medium along the waves as the two waves carry equal energies but in opposite directions.
Thus, when we observe the wave pattern of this superposition, we see that it is characterized by points that appear to be standing still which emphasize one specific frequency that becomes the resultant frequency of the reinforced wave.

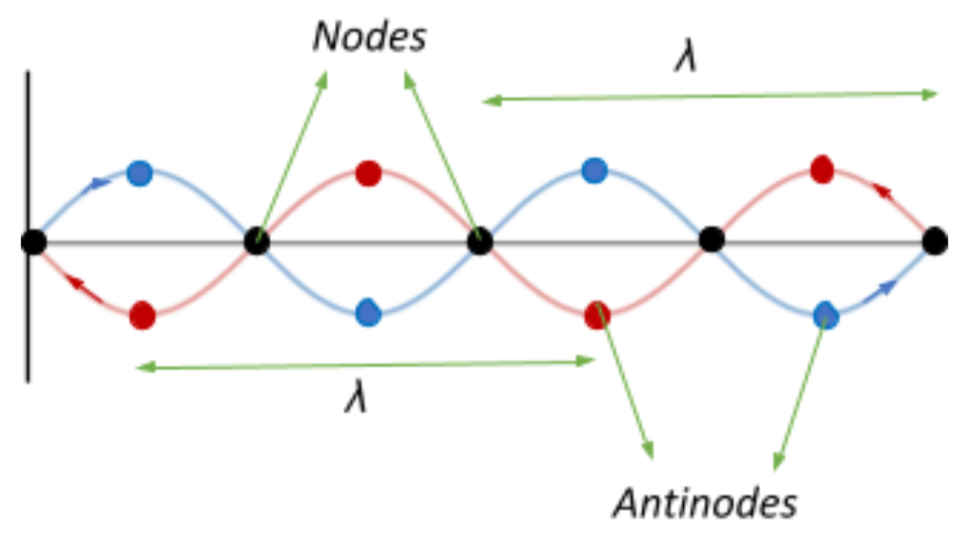
Due to this stationary wave formation, particles at some points of the medium do not vibrate at all. These points of zero amplitude are called nodes. However, particles at some other points of the medium vibrate with maximum amplitude. These points of maximum amplitude are called antinodes. Thus, the amplitude of vibration increases from nodes to antinodes.
In a stationary wave, the nodes and antinodes are alternately produced with a distance between a node and an antinode being $\lambda/4$, and the distance between two successive nodes (or antinodes) is $\lambda/2$, where $\lambda$ is the wavelength of the wave.
Thus, we see that the antinodes signify points of maximum amplitude which is caused by the maximum displacement of the vibrating particle.
Now, a greater amplitude implies more space between the initial and final position of the vibrating particle to allow air to pass through, whereas lesser amplitude means that the air has to squeeze through. Thus, for air passing between two antinodes through a node, it has to first squeeze towards the node and then expand away from it, causing the pressure variation about the node to be maximum.
Thus, we see that a node for displacement is an antinode for pressure and vice versa.
Hence, the correct option for an antinode would be D. Maximum displacement and minimum pressure change.

Note: In general, there are actually two types of stationary waves:
1. Transverse stationary waves: that is produced due to interference of two identical transverse waves traveling along the same path but in opposite directions.
2. Longitudinal stationary waves: that are produced due to interference of two identical longitudinal waves traveling along the same path but in opposite directions.
Also, do not get confused between stationary waves and progressive waves.
Stationary waves are waves at rest whereas progressive waves exhibit motion as they move away from their origin. Particles of the medium vibrate with different amplitudes except at the nodes for stationary waves, whereas each particle of the medium vibrates with the same amplitude for progressive waves. Stationary waves exhibit no energy transfer through the medium whereas energy is transferred through the medium for progressive waves.