Question

In a survey of 80 people it was found that 25 people read Dainik Jagran, 26 read Amar Ujala and 26 read Hindustan. 9 read both Dainik Jagran and Amar Ujala. 11 read Amar Ujala and Hindustan and 8 read Hindustan and Dainik Jagran. 3 read all three newspapers.
Find how many read
(i) None of these
(ii) At least one newspaper
(iii) Exactly one newspaper

Answer 1

Hint: Here, we will use the set formulas to solve this question. We will use the given information and find the different elements of the set formula. Then we will substitute the obtained elements in the formula and solve it further to get the required answers to each of the required parts.

Formula Used:
We will use the following formulas:
1.People who read at least one newspaper: \[n\left( {A \cup B \cup C} \right) = n\left( A \right) + n\left( B \right) + n\left( C \right) - n\left( {A \cap B} \right) - n\left( {B \cap C} \right) - n\left( {A \cap C} \right) + n\left( {A \cap B \cap C} \right)\]
2.People who read exactly one newspaper: \[n\left( {A \cup B \cup C} \right) - n\left( {A \cap B} \right) - n\left( {B \cap C} \right) - n\left( {A \cap C} \right) + 2 \times n\left( {A \cap B \cap C} \right)\]

Complete step-by-step answer:
Total number of people in a survey \[ = 80\]
Now, number of people who read Dainik Jagran, \[n\left( A \right) = 25\]
Number of people, who read Amar Ujala, \[n\left( B \right) = 26\]
And, number of people who read Hindustan, \[n\left( C \right) = 26\]
According to the question,
Number of people, who read both Dainik Jagran and Amar Ujala, \[n\left( {A \cap B} \right) = 9\]
Similarly, number of people who read both read Amar Ujala and Hindustan, \[n\left( {B \cap C} \right) = 11\]
And, the number of people who read both Hindustan and Dainik Jagran, \[n\left( {A \cap C} \right) = 8\]
Also, it is given that the number of people who read all three newspapers, \[n\left( {A \cap B \cap C} \right) = 3\]

(i) To find that how many people read none of the newspapers
Now, we will use the formula:
 \[n\left( {A \cup B \cup C} \right) = n\left( A \right) + n\left( B \right) + n\left( C \right) - n\left( {A \cap B} \right) - n\left( {B \cap C} \right) - n\left( {A \cap C} \right) + n\left( {A \cap B \cap C} \right)\]
Hence, substituting all the values in this formula, we get,
 \[ \Rightarrow n\left( {A \cup B \cup C} \right) = 25 + 26 + 26 - 9 - 11 - 8 + 3\]
 \[ \Rightarrow n\left( {A \cup B \cup C} \right) = 77 - 28 + 3 = 80 - 28 = 52\]
This means that the number of people who read any of the 3 newspapers is 52.
Also, the total number of people in a survey \[ = 80\]
Therefore, number of people who did not read any of the newspapers \[ = 80 - 52 = 28\]
Hence, 28 people do not read any of the newspapers.

(ii) To find that how many people read at least one newspaper
In order to find how many people read at least one newspaper, it means that they can read either one, or two or all the three newspapers.
Hence, the required number of people will be equal to \[n\left( {A \cup B \cup C} \right) = 52\]
Therefore, 52 people read at least one of the newspapers.

(iii) To find that how many people read exactly one newspaper
In order to find this, we will use the formula:
 \[n\left( {A \cup B \cup C} \right) - n\left( {A \cap B} \right) - n\left( {B \cap C} \right) - n\left( {A \cap C} \right) + 2 \times n\left( {A \cap B \cap C} \right)\]
Hence, substituting the values, we get,
People who read exactly one newspaper \[ = 52 - 9 - 11 - 8 + 2\left( 3 \right)\]
 \[ \Rightarrow \] People who read exactly one newspaper \[ = 52 + 6 - 28 = 58 - 28 = 30\]
Therefore, 30 people read exactly one newspaper.
Hence, these are the required answers.

Note: An alternate way to solve this question is by using a Venn diagram.

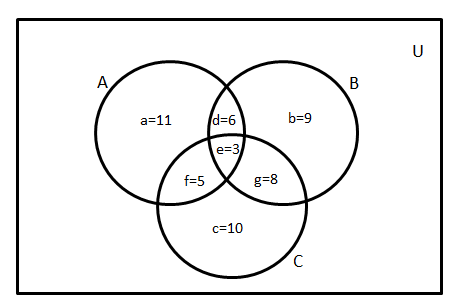
Now, Total number of people in a survey \[ = 80\]
From the diagram,
Now, number of people who read Dainik Jagran,
 \[n\left( A \right) = a + d + f + e = 25\]……………….. \[\left( 1 \right)\]
Number of people, who read Amar Ujala,
 \[n\left( B \right) = b + d + e + g = 26\]……………………………. \[\left( 2 \right)\]
And, number of people who read Hindustan,
 \[n\left( C \right) = c + f + e + g = 26\]…………………….. \[\left( 3 \right)\]
According to the question,
Number of people, who read both Dainik Jagran and Amar Ujala,
  \[n\left( {A \cap B} \right) = d + e = 9\]
Similarly, number of people who read both read Amar Ujala and Hindustan,
 \[n\left( {B \cap C} \right) = e + g = 11\]
And, the number of people who read both Hindustan and Dainik Jagran,
 \[n\left( {A \cap C} \right) = e + f = 8\]
Also, it is given that the number of people who read all three newspapers,
 \[n\left( {A \cap B \cap C} \right) = e = 3\]
Now, substituting \[e = 3\] wherever possible, we get
 \[d + 3 = 9\]
 \[ \Rightarrow d = 6\]
Also,
 \[3 + g = 11\]
 \[ \Rightarrow g = 8\]
And,
 \[3 + f = 8\]
 \[ \Rightarrow f = 5\]
Now, from \[\left( 1 \right)\] , \[a + d + f + e = 25\]
 \[ \Rightarrow a + 6 + 5 + 3 = 25\]
 \[ \Rightarrow a = 25 - 14 = 11\]
Also, from \[\left( 2 \right)\] , \[b + d + e + g = 26\]
 \[ \Rightarrow b + 6 + 3 + 8 = 26\]
 \[ \Rightarrow b = 26 - 17 = 9\]
And, from \[\left( 3 \right)\] , \[c + f + e + g = 26\]
 \[ \Rightarrow c + 5 + 3 + 8 = 26\]
 \[ \Rightarrow c = 26 - 16 = 10\]

(i) To find that how many people read none of the newspapers
First of all we will add the number of people who read any of the newspapers.
 \[ \Rightarrow a + b + c + d + e + f + g = 11 + 9 + 10 + 6 + 3 + 5 + 8 = 52\]
Now, Total number of people in a survey \[ = 80\]
Hence, number of people who do not read any newspaper \[ = 80 - 52 = 28\]

(ii) To find that how many people read at least one newspaper
In order to find how many people read at least one newspaper, it means that they can read either one, or two or all the three newspapers.
Hence, our answer will be the summation of \[a + b + c + d + e + f + g = 11 + 9 + 10 + 6 + 3 + 5 + 8 = 52\]
Hence, 52 people read at least one of the newspapers.

(iii) To find that how many people read exactly one newspaper
Clearly, from the Venn diagram, this will be equal to the summation of \[a + b + c = 11 + 9 + 10 = 30\]
Therefore, 30 people read exactly one newspaper.
Hence, these are the required answers.