Question

In a transformer, the number of turns of primary coil and secondary coil are 5 and 4 respectively. If 220V is applied on the primary coil, then the ratio of primary current to the secondary current is
A. 4 : 5
B. 5 : 4
C. 5 : 9
D. 9 : 5

Answer 1

Hint: A transformer is used to increase or decrease the voltage or current of the input circuit. The ratio of the primary current to the secondary current is equal to the ratio of number of turns in secondary coil to the number of turns in primary coil.
Formula used:
$\dfrac{{{i}_{s}}}{{{i}_{p}}}=\dfrac{{{N}_{p}}}{{{N}_{s}}}$

Complete answer:
Let us first understand what a transformer is.
A transformer is a device that is used to either to lower the voltage of the input circuit or to increase the input voltage circuit. The input circuit is the primary circuit and the output circuit is called the secondary coil.
Each of the circuits consists of a coil with a specific number of turns. The coil of the primary circuit is called a primary coil and the coil of the secondary circuit is called a secondary coil.

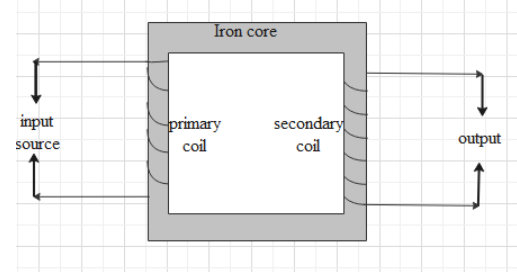
The ratio of secondary to primary voltages depends on the number of turns in both the coils.
Let the secondary and primary voltage be ${{v}_{s}}$ and ${{v}_{p}}$. Let the number of turns be in the secondary and the primary coil be ${{N}_{s}}$ and ${{N}_{p}}$.
Then,
$\dfrac{{{V}_{s}}}{{{V}_{p}}}=\dfrac{{{N}_{s}}}{{{N}_{p}}}$ …… (i)
The ratio of the currents in the secondary and the primary coils respectively are given as $\dfrac{{{i}_{s}}}{{{i}_{p}}}=\dfrac{{{N}_{p}}}{{{N}_{s}}}$ ….. (ii).
It is given that the number of turns of primary coil and secondary coil are 5 and 4 respectively. Therefore, $\dfrac{{{N}_{p}}}{{{N}_{s}}}=\dfrac{5}{4}$.
Substitute this value in equation (ii).
$\Rightarrow \dfrac{{{i}_{s}}}{{{i}_{p}}}=\dfrac{5}{4}$
$\Rightarrow \dfrac{{{i}_{p}}}{{{i}_{s}}}=\dfrac{4}{5}$
This means that the ratio of primary current to the secondary current is 4 : 5.

Hence, the current option is A.

Note:
Multiply the equations (i) and (ii). Then, we get that
 $\dfrac{{{V}_{s}}{{i}_{s}}}{{{V}_{p}}{{i}_{p}}}=\dfrac{{{N}_{s}}}{{{N}_{p}}}.\dfrac{{{N}_{p}}}{{{N}_{s}}}$
$\Rightarrow \dfrac{{{V}_{s}}{{i}_{s}}}{{{V}_{p}}{{i}_{p}}}=1$ …(1).
We know that the product of voltage and the current in the circuit is equal to the power of the circuit.
Therefore,
 $\dfrac{{{V}_{s}}{{i}_{s}}}{{{V}_{p}}{{i}_{p}}}=\dfrac{{{P}_{s}}}{{{P}_{p}}}$ ….(2).
From (1) and (2), we get,
$\dfrac{{{P}_{s}}}{{{P}_{p}}}=1$
${{P}_{s}}={{P}_{p}}$.
This means that power of the input circuit is equal to the power of the output circuit.
However, in reality, there is some energy loss and the output power is less than the input power.
Hence, the above relations are true only for an ideal transformer.