Question

In a triangle $ABC$, find $\angle A$, given $\angle B = {45^ \circ }$

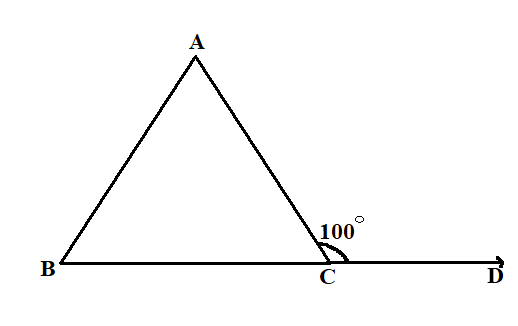
Answer 1

Hint: We will first find the value of $\angle ACB$ by using the property that the angles on the same line have sum ${180^ \circ }$. Next, we will use angle sum property on triangle $ABC$, which will give us $\angle A + \angle B + \angle ACB = {180^ \circ }$. Substitute the known values and then find the value of $\angle A$.

Complete step-by-step answer:
We have the value of $\angle B = {45^ \circ }$ and $\angle ACD = {100^ \circ }$
We have to find the value of $\angle A$
First , we will find the value of $\angle ACB = {100^ \circ }$
We can see that the angles $\angle ACB$ and $\angle ACD$ are on same line, thus the sum of these angles is ${180^ \circ }$
$\angle ACB + \angle ACD = {180^ \circ }$
Now, we will substitute the value of $\angle ACD = {100^ \circ }$
$
  \angle ACB + {100^ \circ } = {180^ \circ } \\
   \Rightarrow \angle ACB = {180^ \circ } - {100^ \circ } \\
   \Rightarrow \angle ACB = {80^ \circ } \\
$
Now, we know that the sum of angles of a triangle is ${180^ \circ }$ by angle sum property of a triangle.
Then,
$\angle A + \angle B + \angle ACB = {180^ \circ }$
We will now substitute the value of $\angle B = {45^ \circ }$ and $\angle ACB = {80^ \circ }$ in the above equation to find the value of $\angle A$
$
  \angle A + {45^ \circ } + {80^ \circ } = {180^ \circ } \\
   \Rightarrow \angle A = {180^ \circ } - \left( {{{45}^ \circ } + {{80}^ \circ }} \right) \\
   \Rightarrow \angle A = {55^ \circ } \\
$

Note: We can also calculate the value of $\angle A$ using the property that the sum of two interior angles is equal to the opposite exterior angle. Then, we can write, $\angle A + \angle B = \angle ACD$. We can then substitute the known values to find the value of $\angle A$.
$
  \angle A + {45^ \circ } = {100^ \circ } \\
   \Rightarrow \angle A = {100^ \circ } - {45^ \circ } \\
   \Rightarrow \angle A = {55^ \circ } \\
$