Question

In a triangle ABC, side AB has the equation 2x + 3y = 29 and the side AC has the equation x + 2y = 16. If the midpoint of BC is (5, 6), then the equation of BC is
$
  (a){\text{ 2x + y = 7}} \\
  (b){\text{ x + y = 1}} \\
  (c){\text{ 2x - y = 17}} \\
  (d){\text{ None of these}} \\
$

Answer 1

Hint – In this problem let the coordinates of B = ($x_1, y_1$) and C = ($x_2, y_2$). Use the midpoint formula to get the relation between these unknown coordinates. Now point C satisfies the equation of line AC and similarly point B satisfies the equation of line AB. This will help getting the value of B = ($x_1, y_1$) and C = ($x_2, y_2$) and thus equation of line BC can be formulated.

Complete step-by-step solution -

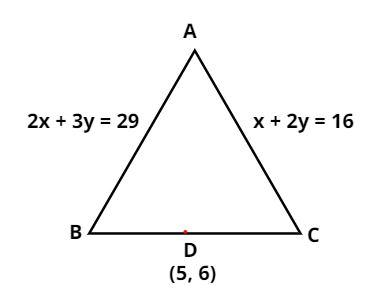
Triangle ABC is shown above, let D be the midpoint of BC.
D = (5, 6)
Equation of line AB = 2x + 3y =29
And equation of line AC = x + 2y = 16
Let B = ($x_1, y_1$) and C = ($x_2, y_2$)
D is the midpoint of BC so apply midpoint formula we have,
$\left( {5,6} \right) = \left( {\dfrac{{{x_1} + {x_2}}}{2},\dfrac{{{y_1} + {y_2}}}{2}} \right)$
Now on simplifying we have,
$ \Rightarrow {x_1} + {x_2} = 10$..................... (1)
$ \Rightarrow {y_1} + {y_2} = 12$......................... (2)
Now the point B satisfying the equation of AB
$ \Rightarrow 2{x_1} + 3{y_1} = 29$................... (3)
And the point C satisfies the equation AC
$ \Rightarrow {x_2} + 2{y_2} = 16$.................... (4)
Now from equation (1) and (2) we have,
${x_1} = 10 - {x_2},{y_1} = 12 - {y_2}$
Substitute this value in equation (3) we have,
$ \Rightarrow 2\left( {10 - {x_2}} \right) + 3\left( {12 - {y_2}} \right) = 29$
Now simplify this we have,
$ \Rightarrow 2{x_2} + 3{y_2} = 20 + 36 - 29 = 27$................... (5)
Now from equation (4) we have,
$ \Rightarrow {x_2} = 16 - 2{y_2}$....................... (6)
Substitute this value in equation (5) we have,
$ \Rightarrow 2\left( {16 - 2{y_2}} \right) + 3{y_2} = 27$
Now simplify this we have,
$ \Rightarrow {y_2} = 32 - 27 = 5$
Substitute this value in equation (6) we have,
$ \Rightarrow {x_2} = 16 - 2\left( 5 \right) = 16 - 10 = 6$
Now Substitute the value of $x_2$ and $y_2$ in equation (1) and (2) we have,
$ \Rightarrow {x_1} + 6 = 10$
$ \Rightarrow {x_1} = 4$
And
$ \Rightarrow {y_1} + 5 = 12$
$ \Rightarrow {y_1} = 7$
So the points B and C are
B = (4, 7) and C = (6, 5)
Now as we know that the equation of line passing through two points ($x_1, y_1$), ($x_2, y_2$) is given as
$ \Rightarrow \left( {y - {y_1}} \right) = \dfrac{{{y_2} - {y_1}}}{{{x_2} - {x_1}}}\left( {x - {x_1}} \right)$
B = ($x_1, y_1$) = (4, 7)
And C = ($x_2, y_2$) = (6, 5)
So the equation of BC is
$ \Rightarrow \left( {y - 7} \right) = \dfrac{{5 - 7}}{{6 - 4}}\left( {x - 4} \right)$
Now simplify the above equation we have,
$ \Rightarrow \left( {y - 7} \right) = \dfrac{{ - 2}}{2}\left( {x - 4} \right)$
$ \Rightarrow y - 7 = - x + 4$
$ \Rightarrow x + y = 7 + 4 = 11$
So this is the required equation of line BC.
Hence option (D) none of these is correct.

Note – Diagrammatic representation of the given information becomes an important part while solving problems of this kind as the geometry helps us to understand which point satisfies which line. The formula used to find equation of line BC $\left( {y - {y_1}} \right) = \dfrac{{{y_2} - {y_1}}}{{{x_2} - {x_1}}}\left( {x - {x_1}} \right)$ is important and the term $\dfrac{{{y_2} - {y_1}}}{{{x_2} - {x_1}}}$ corresponds to the slope of this BC.