Question

In a triangle ABC with $\angle BCA = 90^\circ $, the perpendicular bisector of AB intersects segments AB and AC at X and Y , respectively. If the ratio of the area of quadrilateral BXYC to the area of triangle ABC is $13:18$ and $BC = 12$, then what is the length of AC?

Answer 1

Hint: We will use a three step process to solve this problem. In the first step, we will find the ratio of area of triangle AYX to area of triangle ABC by using the given ratio of the area of quadrilateral BXYC to the area of triangle ABC. In the second step, we will use the area of similar triangle theorems. And finally, we will use the Pythagoras theorem to get our final answer.

Complete step-by-step answer:
We can draw the diagram of the given representation as shown in the figure below.

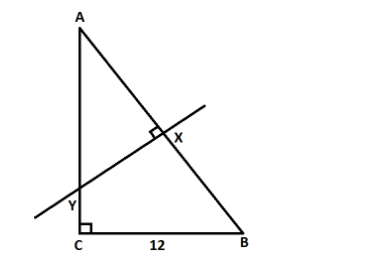
It is given that the ratio of the area of quadrilateral BXYC to the area of triangle ABC is $13:18$.
It is clear from the diagram that
 \[Area{\text{ }}of{\text{ }}ABC = Area{\text{ }}of{\text{ }}AYX + Area{\text{ }}of{\text{ }}BXYC\]
Dividing both the sides by Area of ABC
 \[ \Rightarrow 1 = \dfrac{{Area{\text{ }}of{\text{ }}AYX}}{{Area{\text{ }}of{\text{ }}ABC}} + \dfrac{{{\text{ }}Area{\text{ }}of{\text{ }}BXYC}}{{Area{\text{ }}of{\text{ }}ABC}}\]
 \[ \Rightarrow 1 = \dfrac{{Area{\text{ }}of{\text{ }}AYX}}{{Area{\text{ }}of{\text{ }}ABC}} + \dfrac{{13}}{{18}}\]
 \[ \Rightarrow \dfrac{{Area{\text{ }}of{\text{ }}AYX}}{{Area{\text{ }}of{\text{ }}ABC}} = 1 - \dfrac{{13}}{{18}}\]
 \[ \Rightarrow \dfrac{{Area{\text{ }}of{\text{ }}AYX}}{{Area{\text{ }}of{\text{ }}ABC}} = \dfrac{5}{{18}}\]
From the diagram, we can say that ABC and AYX are similar triangles.
As per the theorem of area of similar triangles, the ratio of the areas of two similar triangles is the same as the ratio of the square of their sides.
 \[ \Rightarrow \dfrac{{A{X^2}}}{{A{C^2}}} = \dfrac{5}{{18}}\]
As XY is the perpendicular bisector of AB, $AX = \dfrac{{AB}}{2}$
 \[
   \Rightarrow \dfrac{{{{\left( {\dfrac{{AB}}{2}} \right)}^2}}}{{A{C^2}}} = \dfrac{5}{{18}} \\
   \Rightarrow \dfrac{{A{B^2}}}{{4 \times A{C^2}}} = \dfrac{5}{{18}} \;
 \]
Now, in right angle triangle ABC with $\angle BCA = 90^\circ $, as per the Pythagoras law,
$A{B^2} = A{C^2} + B{C^2} = A{C^2} + {12^2}$
 \[
   \Rightarrow \dfrac{{A{C^2} + {{12}^2}}}{{4 \times A{C^2}}} = \dfrac{5}{{18}} \\
   \Rightarrow 18A{C^2} + \left( {18 \times {{12}^2}} \right) = 20A{C^2} \\
   \Rightarrow 2A{C^2} = 18 \times {12^2} \\
   \Rightarrow A{C^2} = 9 \times {12^2} \\
   \Rightarrow A{C^2} = {3^2} \times {12^2} \\
   \Rightarrow AC = 36 \;
 \]
Thus, the length of AC is 36.
So, the correct answer is “36”.

Note: In this type of question, we need to analyze the given data and think of useful theorems which can be applied to get to the answers easily. For example, here, we have applied two theorems. First, area of similar triangle theorem and then Pythagoras theorem to determine our final answer, the length of AC.