Question

In a triangle \[\Delta ABC\] a point ‘D’ on side ‘BC’ is such that \[DC=6,BC=15\] find the ratios
(i) \[A\left( \Delta ABD \right):A\left( \Delta ABC \right)\]
(ii) \[A\left( \Delta ABD \right):A\left( \Delta ADC \right)\]

Answer 1

Hint: We solve this problem first by drawing the height from vertex ‘A’ to side ‘BC’. The diagram representing the given data is shown below.

Here the length ‘AE’ will be the height for all the triangles that can be seen in the figure because ‘A’ is a common vertex for all triangles and ‘E’ lies on the base of all triangles. then we use the area formula of triangle given as
\[A=\dfrac{1}{2}\left( \text{Base} \right)\left( \text{Height} \right)\]
By using the above formula we find the required ratios.

Complete step-by-step answer:
We are given that there is a point ‘D’ on ‘BC’ such that
\[\Rightarrow BC=15\]
\[\Rightarrow DC=6\]
Let us assume that a perpendicular drawn from the vertex ‘A’ to side ‘BC’ as shown in the figure.

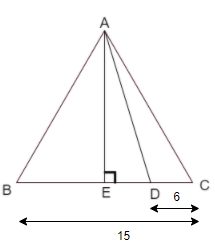
Here, we can see that the line ‘AE’ is the height for all three triangles \[\Delta ABC,\Delta ABD,\Delta ADC\]
Now, let us solve for the first part
(i) \[A\left( \Delta ABD \right):A\left( \Delta ABC \right)\]
We know that the formula for area of triangle is given as
\[A=\dfrac{1}{2}\left( \text{Base} \right)\left( \text{Height} \right)\]
Let us consider the triangle \[\Delta ABD\]
By using the area formula the area of triangle \[\Delta ABD\] we get
\[\Rightarrow A\left( \Delta ABD \right)=\dfrac{1}{2}\left( BD \right)\left( AE \right)..........equation(i)\]
Now, let us consider the triangle \[\Delta ABC\]
By using the area formula the area of triangle \[\Delta ABC\] we get
\[\Rightarrow A\left( \Delta ABC \right)=\dfrac{1}{2}\left( BC \right)\left( AE \right)..........equation(ii)\]
Now, by dividing the equation (i) with equation (ii) we get
\[\begin{align}
  & \Rightarrow \dfrac{A\left( \Delta ABD \right)}{A\left( \Delta ABC \right)}=\dfrac{\dfrac{1}{2}\times BD\times AE}{\dfrac{1}{2}\times BC\times AE} \\
 & \Rightarrow \dfrac{A\left( \Delta ABD \right)}{A\left( \Delta ABC \right)}=\dfrac{BD}{BC} \\
\end{align}\]
By substituting the required values in above equation we get
\[\begin{align}
  & \Rightarrow \dfrac{A\left( \Delta ABD \right)}{A\left( \Delta ABC \right)}=\dfrac{6}{15} \\
 & \Rightarrow \dfrac{A\left( \Delta ABD \right)}{A\left( \Delta ABC \right)}=\dfrac{2}{5} \\
\end{align}\]
We know that the ratio definition that is
\[\Rightarrow a:b=\dfrac{a}{b}\]
Therefore, by using the ratio theorem to above equation we get
\[\therefore A\left( \Delta ABD \right):A\left( \Delta ABC \right)=2:5\]
Now, let us solve for second part
(ii) \[A\left( \Delta ABD \right):A\left( \Delta ADC \right)\]
We know that the formula for area of triangle is given as
\[A=\dfrac{1}{2}\left( \text{Base} \right)\left( \text{Height} \right)\]
Let us consider the triangle \[\Delta ABD\]
By using the area formula the area of triangle \[\Delta ABD\] we get
\[\Rightarrow A\left( \Delta ABD \right)=\dfrac{1}{2}\left( BD \right)\left( AE \right)..........equation(i)\]
Now, let us consider the triangle \[\Delta ADC\]
By using the area formula the area of triangle \[\Delta ADC\] we get
\[\Rightarrow A\left( \Delta ADC \right)=\dfrac{1}{2}\left( DC \right)\left( AE \right)..........equation(iii)\]
Now, by dividing the equation (i) with equation (iii) we get
\[\begin{align}
  & \Rightarrow \dfrac{A\left( \Delta ABD \right)}{A\left( \Delta ADC \right)}=\dfrac{\dfrac{1}{2}\times BD\times AE}{\dfrac{1}{2}\times DC\times AE} \\
 & \Rightarrow \dfrac{A\left( \Delta ABD \right)}{A\left( \Delta ADC \right)}=\dfrac{BD}{DC}........equation(iv) \\
\end{align}\]
Here, we know that the point ‘D’ divides the side ‘BC’ in two parts that is
\[\begin{align}
  & \Rightarrow BC=BD+DC \\
 & \Rightarrow 15=BD+6 \\
 & \Rightarrow BD=9 \\
\end{align}\]
Now, by substituting the required values in equation (iv) we get
\[\begin{align}
  & \Rightarrow \dfrac{A\left( \Delta ABD \right)}{A\left( \Delta ADC \right)}=\dfrac{9}{6} \\
 & \Rightarrow \dfrac{A\left( \Delta ABD \right)}{A\left( \Delta ADC \right)}=\dfrac{3}{2} \\
\end{align}\]


We know that the ratio definition that is
\[\Rightarrow a:b=\dfrac{a}{b}\]
Therefore, by using the ratio theorem to above equation we get
\[\therefore A\left( \Delta ABD \right):A\left( \Delta ADC \right)=3:2\]

Note: We can solve the second part in another method also.
From the first part we have the ratio
\[\Rightarrow A\left( \Delta ABD \right):A\left( \Delta ABC \right)=2:5\]
\[\Rightarrow A\left( \Delta ABC \right):A\left( \Delta ABD \right)=5:2\]
Now by converting ratio to division we get
\[\Rightarrow \dfrac{A\left( \Delta ABC \right)}{A\left( \Delta ADC \right)}=\dfrac{5}{2}.........equation(v)\]
We know that when a line divides the triangle into two parts then the total area of triangle will be sum of those two parts that is from the figure
\[\Rightarrow A\left( \Delta ABC \right)=A\left( \Delta ABD \right)+A\left( \Delta ADC \right)\]
By substituting the above equation in equation (v) we get
\[\begin{align}
  & \Rightarrow \dfrac{A\left( \Delta ABD \right)+A\left( \Delta ADC \right)}{A\left( \Delta ADC \right)}=\dfrac{5}{2} \\
 & \Rightarrow \dfrac{A\left( \Delta ABD \right)}{A\left( \Delta ADC \right)}+1=\dfrac{5}{2} \\
 & \Rightarrow \dfrac{A\left( \Delta ABD \right)}{A\left( \Delta ADC \right)}=\dfrac{3}{2} \\
\end{align}\]
By converting into ratio we get
\[\therefore A\left( \Delta ABD \right):A\left( \Delta ADC \right)=3:2\]