Answer
487.5k+ views
Hint: For solving this question, first we will see the result of the Basic Proportionality theorem. After that, we will use it for $\Delta ABC$, $\Delta ADC$. Then, we will solve accordingly to prove the desired result easily.
Complete step-by-step solution -
Given:
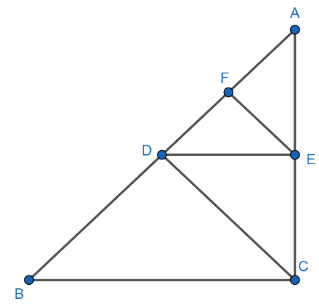
It is given that, there is $\Delta ABC$, $DE\parallel BC$ and $CD\parallel EF$ for the following figure:
To Prove: We have to prove that, $A{{D}^{2}}=AF\times AB$.
Now, before proceeding we should understand an important theorem which is called the Basic Proportionality theorem.
Basic Proportionality Theorem $\left( BPT \right)$ :
Consider a $\Delta ABC$ and a line PQ parallel to the side BC intersects side AB at Q and side AC at P. For more clarity look at the figure given below:
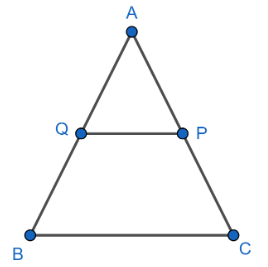
Now, as PQ is parallel to the side BC so, $\angle AQP=\angle ABC$ and $\angle APQ=\angle ACB$ as they are corresponding angles.
Now, consider $\Delta ABC$ and $\Delta AQP$ . Then,
$\begin{align}
& \angle BAC=\angle QAP\text{ }\left( common \right) \\
& \angle AQP=\angle ABC\text{ }\left( corresponding\text{ }angles \right) \\
& \angle APQ=\angle ACB\text{ }\left( corresponding\text{ }angles \right) \\
\end{align}$
Now, as all the angles of the triangles are equal so, $\Delta ABC\sim \Delta AQP$ . And we know that for every similar triangles ratio of the corresponding sides is equal. Then,
$\dfrac{AB}{AQ}=\dfrac{AC}{AP}=\dfrac{QP}{BC}$
Now, from the Basic Proportionality theorem, we say that if PQ is drawn parallel to the side BC and it intersects side AB at Q and side AC at P. Then,
$\dfrac{AB}{AQ}=\dfrac{AC}{AP}=\dfrac{QP}{BC}$
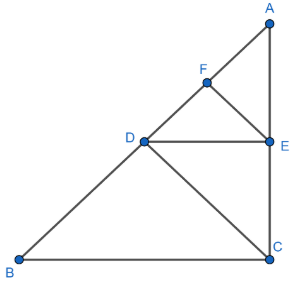
Now, we come back to our problem in which we have the following figure:
Now, we consider $\Delta ABC$ in which $DE\parallel BC$. Then,
$\dfrac{AD}{AB}=\dfrac{AE}{AC}\text{ }(BPT)..................\left( 1 \right)$
Now, we consider $\Delta ADC$ in which $CD\parallel EF$. Then,
$\dfrac{AF}{AD}=\dfrac{AE}{AC}\text{ }(BPT)..................\left( 2 \right)$
Now, we will equate the equation (1) and (2). Then,
$\begin{align}
& \dfrac{AD}{AB}=\dfrac{AE}{AC}=\dfrac{AF}{AD} \\
& \Rightarrow \dfrac{AD}{AB}=\dfrac{AF}{AD} \\
& \Rightarrow AD\times AD=AF\times AB \\
& \Rightarrow A{{D}^{2}}=AF\times AB \\
\end{align}$
Now, from the above result, we conclude that for the given triangle $A{{D}^{2}}=AF\times AB$.
Hence, proved.
Note: Here, the student should first understand what is asked in the question and then proceed in the right direction to get the correct answer quickly. After that, we should not be confused while applying the result of the Basic proportionality theorem, and we should proceed stepwise to avoid confusion. Moreover, while solving such questions, we should always refer to the diagram if we get stuck at some step and try to figure out the best way to solve it.
Complete step-by-step solution -
Given:
It is given that, there is $\Delta ABC$, $DE\parallel BC$ and $CD\parallel EF$ for the following figure:

To Prove: We have to prove that, $A{{D}^{2}}=AF\times AB$.
Now, before proceeding we should understand an important theorem which is called the Basic Proportionality theorem.
Basic Proportionality Theorem $\left( BPT \right)$ :
Consider a $\Delta ABC$ and a line PQ parallel to the side BC intersects side AB at Q and side AC at P. For more clarity look at the figure given below:

Now, as PQ is parallel to the side BC so, $\angle AQP=\angle ABC$ and $\angle APQ=\angle ACB$ as they are corresponding angles.
Now, consider $\Delta ABC$ and $\Delta AQP$ . Then,
$\begin{align}
& \angle BAC=\angle QAP\text{ }\left( common \right) \\
& \angle AQP=\angle ABC\text{ }\left( corresponding\text{ }angles \right) \\
& \angle APQ=\angle ACB\text{ }\left( corresponding\text{ }angles \right) \\
\end{align}$
Now, as all the angles of the triangles are equal so, $\Delta ABC\sim \Delta AQP$ . And we know that for every similar triangles ratio of the corresponding sides is equal. Then,
$\dfrac{AB}{AQ}=\dfrac{AC}{AP}=\dfrac{QP}{BC}$
Now, from the Basic Proportionality theorem, we say that if PQ is drawn parallel to the side BC and it intersects side AB at Q and side AC at P. Then,
$\dfrac{AB}{AQ}=\dfrac{AC}{AP}=\dfrac{QP}{BC}$
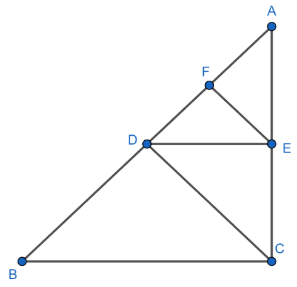
Now, we come back to our problem in which we have the following figure:

Now, we consider $\Delta ABC$ in which $DE\parallel BC$. Then,
$\dfrac{AD}{AB}=\dfrac{AE}{AC}\text{ }(BPT)..................\left( 1 \right)$
Now, we consider $\Delta ADC$ in which $CD\parallel EF$. Then,
$\dfrac{AF}{AD}=\dfrac{AE}{AC}\text{ }(BPT)..................\left( 2 \right)$
Now, we will equate the equation (1) and (2). Then,
$\begin{align}
& \dfrac{AD}{AB}=\dfrac{AE}{AC}=\dfrac{AF}{AD} \\
& \Rightarrow \dfrac{AD}{AB}=\dfrac{AF}{AD} \\
& \Rightarrow AD\times AD=AF\times AB \\
& \Rightarrow A{{D}^{2}}=AF\times AB \\
\end{align}$
Now, from the above result, we conclude that for the given triangle $A{{D}^{2}}=AF\times AB$.
Hence, proved.
Note: Here, the student should first understand what is asked in the question and then proceed in the right direction to get the correct answer quickly. After that, we should not be confused while applying the result of the Basic proportionality theorem, and we should proceed stepwise to avoid confusion. Moreover, while solving such questions, we should always refer to the diagram if we get stuck at some step and try to figure out the best way to solve it.
Recently Updated Pages
How is abiogenesis theory disproved experimentally class 12 biology CBSE

What is Biological Magnification

Choose the word opposite in meaning to the given word class 8 english CBSE

Choose the word opposite in meaning to the given word class 8 english CBSE

Choose the word opposite in meaning to the given word class 8 english CBSE

Choose the word opposite in meaning to the given word class 8 english CBSE

Trending doubts
When people say No pun intended what does that mea class 8 english CBSE

State the differences between manure and fertilize class 8 biology CBSE

Who is known as Tutie Hind A Saint Kabir B Amir Khusro class 8 social science CBSE

Advantages and disadvantages of science

Write a letter to the Municipal Commissioner to inform class 8 english CBSE

What is BLO What is the full form of BLO class 8 social science CBSE