Question

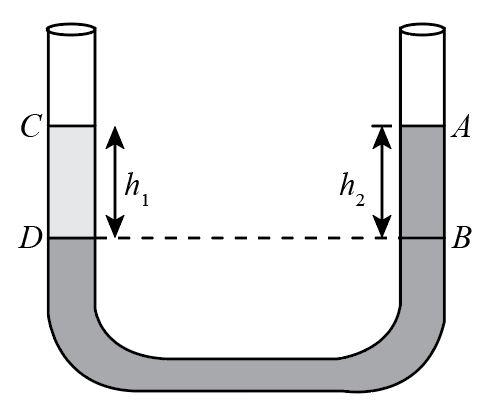
In a U-tube experiment, a column AB of water is balanced by a column CD of paraffin. The relative density of paraffin is:

$\begin{array}{l}
A.\,\,\,\dfrac{{{h_2}}}{{{h_1}}}\\
B.\,\,\,\dfrac{{{h_1}}}{{{h_2}}}\\
C.\,\,\,\dfrac{{{h_2} - {h_1}}}{{{h_1}}}\\
D.\,\,\,\dfrac{{{h_2}}}{{{h_1} + {h_2}}}
\end{array}$

Answer 1

Hint: This question tests us of our knowledge of fluid dynamics. Here we have to use the condition of the U-tube and the condition of a balanced U-tube. And then we will use that condition to find the relative density of paraffin.

Complete step by step answer:For a balanced U-Tube the pressure in both the columns is equal. Therefore, the pressure acting due to the liquids in each column is given as:
$P = {P_0} + \rho gh$, where $\rho $ is the density of the liquid, g is the acceleration due to gravity and h is the height of the liquid column and ${P_0}$ is the atmospheric pressure.
Therefore, the pressure in column one is:
${P_{CD}} = {P_0} + {\rho _p}g{h_1}$
And the pressure in the second column is:
${P_{AB}} = {P_0} + {\rho _w}g{h_2}$
And for the condition of balanced U-Tube these two pressure values would be equal.
Equating the above two equations, we will get:
$\begin{array}{l}
{P_{AB}} = {P_{CD}}\\
{P_0} + {\rho _w}g{h_2} = {P_0} + {\rho _{Paraffin}}g{h_1}
\end{array}$
Cancelling the atmospheric pressure ${P_0}$ from the above expression, we get:
${\rho _w}g{h_2} = {\rho _{Paraffin}}g{h_1}$
Now we have a relation involving the density of the paraffin, water and the heights of the water columns.
Now if we consider the formula of relative density of paraffin it is given below:
\[relative\,density = \dfrac{{{\rho _{paraffin}}}}{{{\rho _w}}}\]
Therefore, if we arrange the relation which we derived we can find the relative density of paraffin:
$\begin{array}{l}
{\rho _w}g{h_2} = {\rho _{Paraffin}}g{h_1}\\
\dfrac{{{\rho _{Paraffin}}}}{{{\rho _w}}} = \dfrac{{g{h_2}}}{{g{h_1}}}\\
\dfrac{{{\rho _{Paraffin}}}}{{{\rho _w}}} = \dfrac{{{h_2}}}{{{h_1}}}\\
relative\,density = \dfrac{{{h_2}}}{{{h_1}}}
\end{array}$
Hence, the relative density is $\dfrac{{{h_2}}}{{{h_1}}}$ and the correct option from the given options is (A.)

Note:In questions like these we have to apply concepts of relative quantities which is the ratio of the quantity with the standard quantity. Also, when calculating pressure in a U-tube one should always add the factor of atmospheric pressure.