Question

In a vertical circle of radius $\left( r \right),$ at what point in its path a particle may have tension equal to zero:
A. Highest point
B. Lowest point
C. At any point
D. At a point horizontal from the centre of radius

Answer 1

Hint: While moving in a vertical circle, the particle must satisfy the constraints of centripetal force to remain in a circle, and also satisfy the requirements of conservation of energy as gravitational potential energy of the particle is converted to its kinetic energy when the mass moves downward and kinetic energy is converted to potential energy when mass moves upward in the circle. We will find the tension produced in the wire at different points in the circle by calculating the velocity of the particle at that particular point.

Formula used: Centripetal force, ${{F}_{c}}=\dfrac{m{{v}^{2}}}{r}$

Complete step by step answer:
We are given that a particle attached to a string has to execute circular motion in the path of radius $r$and we have to calculate the point where tension in the string will be zero.
We will first draw the free body diagram of the object in a vertical circular motion.

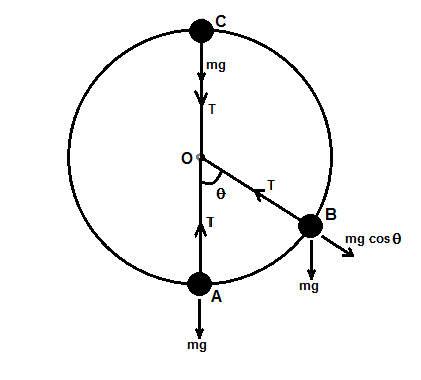
In the free body diagram, we can see that:
1.The gravitational force on the object is always acting vertically, and is equal to the weight of the object.
2. Tension at the object will always be acting radially inwards.
Consider the object put into motion at point A, with an initial velocity $v$
Forces acting on the object will be gravitational force and tension.
At any random point B, constructing the free body diagram of object,
We have gravitational force $mg$ acting on the object vertically down, and a tension force $T$ acting radially.

Now, we will break the gravitational force into two perpendicular components:
1. Tangential component of the gravitational force
2. Radial component of the gravitational force
Consider, the tension or radial vector makes angle $\theta $ with the vertical,
So the component of gravitational force tangential to the circle will be $mg\sin \theta $
And, the component of gravitational force radial to the circle will be $mg\cos \theta ,$ radially outwards.
Now, for the particle to undergo circular motion there must be centripetal force acting on it radially inwards.
We know that, centripetal force acting on a particle of mass $m$ undergoing a circular motion with velocity $v$ in a circle of radius $r$ is:
${{F}_{c}}=\dfrac{m{{v}^{2}}}{r}$
The centripetal force will be provided by the resultant of tension and radial component of gravitational force.
Thus, we have:
\[\dfrac{m{{v}^{2}}}{r}=T-mg\cos \theta ,\]
Now, for tension equal to zero, we have:
$T=0$
Or, \[\dfrac{m{{v}^{2}}}{r}=-mg\cos \theta ,\]
Or, \[{{v}^{2}}=-rg\cos \theta ,\]
Now, for the above condition to be legitimate,
\[-rg\cos \theta \ge 0\]
Or, \[rg\cos \theta \le 0\]
Or, \[\cos \theta \le 0\]
So, we have:
\[{{90}^{o}}\le \theta \le {{270}^{o}}\]
Now, we will consider each option one by one,
At the highest point, \[\theta ={{180}^{o}}\]and it satisfies the condition, \[{{90}^{o}}\le \theta \le {{270}^{o}}\]
Also, \[{{v}^{2}}=-rg\cos \theta ,\]
For, \[\theta ={{180}^{o}}\]at the highest point,
\[{{v}^{2}}=rg\]
Or, $v=\sqrt{rg}$
We know that the minimum initial velocity required at the highest point to get the particle in a complete vertical circular motion is $\sqrt{rg}$
Thus, in this condition, tension can be equal to zero at the highest point with particles undergoing vertical circular motion.
So, the option A is correct
At the lowest point, \[\theta ={{0}^{o}}\]and it doesn’t satisfies the condition, \[{{90}^{o}}\le \theta \le {{270}^{o}}\]
So option B is incorrect.
Tension can’t be zero at any point as we need to satisfy the condition, \[{{90}^{o}}\le \theta \le {{270}^{o}}\]which every point doesn’t satisfy.
So, option C is incorrect.
At a point horizontal from the centre of radius,
\[\theta ={{90}^{o}}\] Or \[\theta ={{270}^{o}}\] and it satisfies the condition, \[{{90}^{o}}\le \theta \le {{270}^{o}}\]
For, \[\theta ={{90}^{o}}\] or \[\theta ={{270}^{o}}\]
We have, $\cos \theta =0$
For tension to be zero at these points,
\[{{v}^{2}}=-rg\cos \theta =0\]
Or, $v=0$
If the velocity of the particle becomes zero at the point where angle \[\theta ={{90}^{o}},\] the particle will not be able to complete its circular motion.
So, option D is incorrect.

So, the correct answer is “Option A”.

Note: Points to remember:
1. As a particle goes round the circle, the tension produced in the string varies, being greatest at the bottom of the circle and least at the top.
2. If the string is to break, it will be at the bottom of the path where it has to not only support the particle but also pull it up out of its straight-line path.
3. The condition for the particle to execute a complete vertical circle without the string is independent of the mass of the particle.
4. It is slightly easier to cause a particle attached to the end of a rigid rod to execute a vertical circle than to cause a particle attached to the end of a string to execute the same circle.