Question

In an examination, 35% students failed in Hindi, 45% students failed in English and 20% students failed in both the subjects. What is the percentage of students passing in both the subjects?

Answer 1

Hint: Here some of the students who failed in Hindi may also fail in English too. We are going to use union of sets to solve the given problem.

Let P(H) is the percentage of students who failed in Hindi and P(E) be the percentage of students who failed in English.
From the given information, we have
Percentage of students failed in Hindi = P (H) = 35%
Percentage of students failed in English = P (E) = 45%
Percentage of students who failed in both subjects = $P(H \cap E)$ =20%
$\because \left( {A \cup B} \right) = \left( A \right) + \left( B \right) - \left( {A \cap B} \right)$ [Union of sets]
The total fail percentage is
$ \Rightarrow P(H \cup E) = P(H) + P(E) - P(H \cap E)$
$ \Rightarrow P(H \cup E) = 35 + 45 - 20 = 60$
$ \Rightarrow $ 60% of students failed in at least one.
In class we have 100% students. Then number of students who passed in both subjects = 100% – 60% = 40%
$\therefore $40% of students passed in both the subjects.

Note:
We need to understand the given information carefully. We can also use Venn diagrams.

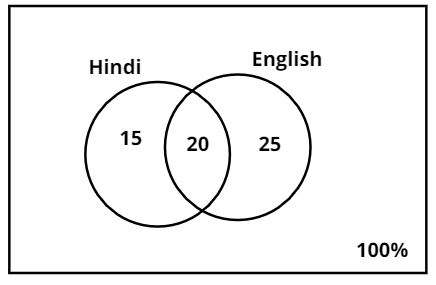
In the above diagram, if we observe we have individual percentages of each set. Percentage of students who failed only in Hindi is 15%, the percentage of students who failed only in English is 25% and the percentage of students who failed in both Hindi and English is 20%. A student will either pass or fail in the subject.
$ \Rightarrow $Pass percentage + fail percentage = 100%
When we get the total failure percentage, we can find the pass percentage easily.