Question

In an examination, 70% of the candidates passed in English, 80% passed in mathematics, and 10% failed in both these subjects. If 144 candidates passed in both then the total number of candidates was
A) $125$
B) $200$
C) $240$
D) $375$

Answer 1

Hint: For solving these types of problems first we need to draw the Venn diagram of the situation by analyzing the statement provided in the problem. After that we assign different values to different parts of the circles. By using this data interpretation, we can easily evaluate our answer.

Complete step by step answer:
It is given in the question stated as, candidates passed $\% $ in English $ = 70\% $
Candidates passed $\% $ in Mathematics $ = 80\% $
Total no. of passed candidates in both the subjects $ = 144$
Total $\% $ failed candidates in both the subjects $ = 10\% $
We have to find out the total number of candidates in the examination.
Firstly, we need to find the number of failed candidates because we know the $\% $ of failed candidates which is $10\% $
We need to convert the passed candidate’s data to failed candidates to get the easier way
Failed candidates in the subject English $ = (100 - 70) = 30\% $
Failed candidates in the subject mathematics $ = (100 - 80) = 20\% $
Percentage of the passed students in both the subjects $ = 100 - (20 + 10 + 10) = 60\% $ ($\because $Using Venn Diagram)
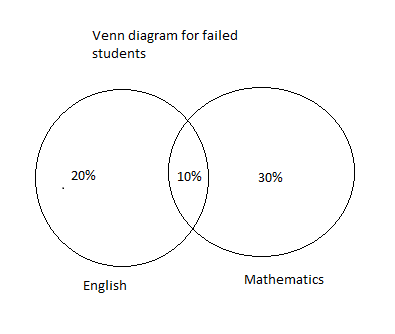
In the Venn diagram
Percentages of the students who failed in English subject $ = 30\% $
Percentages of the students who failed in the Mathematics Subject $ = 20\% $
Percentages of the students who failed in both the subjects Mathematics and English$ = 10\% $
Here the intersection part of the diagram represents the students who failed in both the subjects Mathematics and English.

According to the question, given that
$60\% $ of the students $ = 144$
Now we need to calculate the total students
$\therefore$ Total students $ = \dfrac{{144}}{{60}} \times 100$
After cancellation, the numerator and denominator we get,
$ = 240$

Therefore, the total numbers of students are $240$. Hence, option $(C)$ is the correct answer.

Note:
The key concept is involved in this problem is the knowledge of Venn diagrams. Students must not get confused by seeing the area of the combined circles which is called the intersection part of the circles in the Venn diagram. The above representation is a possible representation but the value on the calculation is the correct value.