Answer
99.9k+ views
Hint: In half deflection method, the value of the resistance across the resistor is such that the deflection made will be half that of the current when the resistance was disconnected. The current is directly proportional to the deflection of a galvanometer pointer.
Formula used: In this solution we will be using the following formulae;
\[G = \dfrac{{RS}}{{R - S}}\] where \[G\] is the resistance of the galvanometer, \[R\] is the resistance in the main circuit and \[S\] is the resistance across the galvanometer
Complete step by step solution:
Generally, the formula using half deflection method the resistance of a galvanometer is given as
\[G = \dfrac{{RS}}{{R - S}}\] where \[G\] is the resistance of the galvanometer, \[R\] is the resistance in the main circuit and \[S\] is the resistance across the galvanometer
Hence, by inserting known values, we have
\[G = \dfrac{{10\left( 4 \right)}}{{10 - 4}} = \dfrac{{40}}{6}\Omega \]
\[ \Rightarrow G = \dfrac{{20}}{3}\Omega \]
Hence, the correct option is A
Note: For clarity, the formula used can be proven as follows:
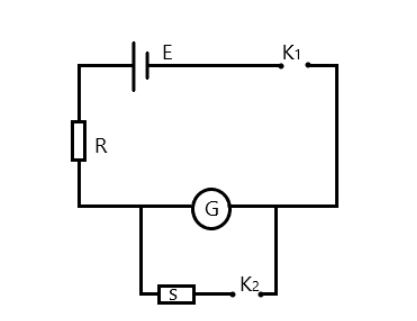
First, let’s assume the key \[{K_1}\] is the only closed key. In this case the current flowing through the circuit, and hence through \[G\] will be
\[{I_G} = \dfrac{E}{{R + G}}\]
Generally, the deflection shown in the galvanometer is proportional to the current flowing through it. Hence,
\[{I_G} = k\theta \]
Then
\[\dfrac{S}{{S + G}}I = \dfrac{{k\theta }}{2}\]
Now, assuming we close the key \[{K_2}\], it can be proven that the current flowing through the galvanometer becomes
\[I{'_G} = \dfrac{S}{{S + G}}I\]where\[I\] is the new current flowing through the main circuit, hence the current flowing through \[R\].
In the half deflection method, the value of S is adjusted such that the deflection is half of the original value when the key \[{K_2}\] was not closed.
Thus,
\[I{'_G} = \dfrac{{k\theta }}{2}\].
\[ \Rightarrow \dfrac{S}{{S + G}}I = \dfrac{{k\theta }}{2}\]
Dividing equation above by \[\dfrac{S}{{S + G}}I = \dfrac{{k\theta }}{2}\], and simplifying, we have
\[\dfrac{{SI(R + G)}}{{E(S + G)}} = \dfrac{1}{2}\]
Now, the equivalent resistance of the circuit is
\[{R_{eq}} = R + \dfrac{{SG}}{{S + G}}\]. Then the current would be
\[I = \dfrac{E}{{{R_{eq}}}} = \dfrac{E}{{R + \dfrac{{SG}}{{S + G}}}}\]
Then substituting into \[\dfrac{{SI(R + G)}}{{E(S + G)}} = \dfrac{1}{2}\] and then simplifying to make \[G\] subject, we have
\[G = \dfrac{{RS}}{{R - S}}\]
Formula used: In this solution we will be using the following formulae;
\[G = \dfrac{{RS}}{{R - S}}\] where \[G\] is the resistance of the galvanometer, \[R\] is the resistance in the main circuit and \[S\] is the resistance across the galvanometer
Complete step by step solution:
Generally, the formula using half deflection method the resistance of a galvanometer is given as
\[G = \dfrac{{RS}}{{R - S}}\] where \[G\] is the resistance of the galvanometer, \[R\] is the resistance in the main circuit and \[S\] is the resistance across the galvanometer
Hence, by inserting known values, we have
\[G = \dfrac{{10\left( 4 \right)}}{{10 - 4}} = \dfrac{{40}}{6}\Omega \]
\[ \Rightarrow G = \dfrac{{20}}{3}\Omega \]
Hence, the correct option is A
Note: For clarity, the formula used can be proven as follows:
First, let’s assume the key \[{K_1}\] is the only closed key. In this case the current flowing through the circuit, and hence through \[G\] will be
\[{I_G} = \dfrac{E}{{R + G}}\]
Generally, the deflection shown in the galvanometer is proportional to the current flowing through it. Hence,
\[{I_G} = k\theta \]
Then
\[\dfrac{S}{{S + G}}I = \dfrac{{k\theta }}{2}\]
Now, assuming we close the key \[{K_2}\], it can be proven that the current flowing through the galvanometer becomes
\[I{'_G} = \dfrac{S}{{S + G}}I\]where\[I\] is the new current flowing through the main circuit, hence the current flowing through \[R\].
In the half deflection method, the value of S is adjusted such that the deflection is half of the original value when the key \[{K_2}\] was not closed.
Thus,
\[I{'_G} = \dfrac{{k\theta }}{2}\].
\[ \Rightarrow \dfrac{S}{{S + G}}I = \dfrac{{k\theta }}{2}\]
Dividing equation above by \[\dfrac{S}{{S + G}}I = \dfrac{{k\theta }}{2}\], and simplifying, we have
\[\dfrac{{SI(R + G)}}{{E(S + G)}} = \dfrac{1}{2}\]
Now, the equivalent resistance of the circuit is
\[{R_{eq}} = R + \dfrac{{SG}}{{S + G}}\]. Then the current would be
\[I = \dfrac{E}{{{R_{eq}}}} = \dfrac{E}{{R + \dfrac{{SG}}{{S + G}}}}\]
Then substituting into \[\dfrac{{SI(R + G)}}{{E(S + G)}} = \dfrac{1}{2}\] and then simplifying to make \[G\] subject, we have
\[G = \dfrac{{RS}}{{R - S}}\]
Recently Updated Pages
Write a composition in approximately 450 500 words class 10 english JEE_Main

Arrange the sentences P Q R between S1 and S5 such class 10 english JEE_Main

Write an article on the need and importance of sports class 10 english JEE_Main

Name the scale on which the destructive energy of an class 11 physics JEE_Main

Choose the exact meaning of the given idiomphrase The class 9 english JEE_Main

Choose the one which best expresses the meaning of class 9 english JEE_Main

Other Pages
The values of kinetic energy K and potential energy class 11 physics JEE_Main

Electric field due to uniformly charged sphere class 12 physics JEE_Main

BF3 reacts with NaH at 450 K to form NaF and X When class 11 chemistry JEE_Main

Dependence of intensity of gravitational field E of class 11 physics JEE_Main

In the reaction of KMnO4 with H2C204 20 mL of 02 M class 12 chemistry JEE_Main

What torque will increase the angular velocity of a class 11 physics JEE_Main