
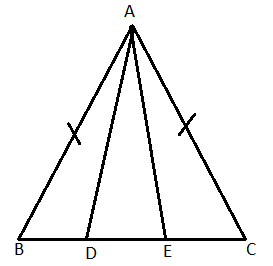
In an isosceles triangle ABC with AB = AC, D and E are points on BC such that BE = CD. Show that AD = AE.

Answer
430.9k+ views
2 likes
Hint: Use the property given as “Angles of equal opposite sides are equal in a triangle”, to prove the triangles ABD and C.P.C.T prove the sides AD and AE are equal to each other.
Complete step-by-step answer:
As we have an isosceles triangle ABC with AB = AC, where D and E are points on BC such that BE = CD and we need to prove that the sides AD and AE are equal i.e. AD = AE.
So, diagram can be given as
So, we have
AB = AC……………..(i)
BE = CD…………….(ii)
Now, we know the property of triangles that opposite angles of the opposite sides are equal if sides are equal. It means
And from equation (ii), we (iii) have BE = CD
Now, subtract DE from both sides of terms of the above equation. So, we get
BE – DE = CD – DE
Now, we can observe that the diagram is replaced by side BD and CD – DE by side CE. Hence, we get above equation as
BD = CE………………….(iv)
Now, in
AB = AC (from equation (i))
BD = CE (from equation (iv))
Hence,
So, now all the corresponding sides and angles of triangles ABD and ACE are equal by the C.P.C.T property of congruent triangles.
Hence, we get
AD = AE ( C.P.C.T)
So, it proved that AD and AE are equal.
Note: Another approach for proving AD = AE, we can prove the triangles ABE and ADE as congruent triangle in the following way:
AB = AC
BE = DC
By SAS criteria
Complete step-by-step answer:
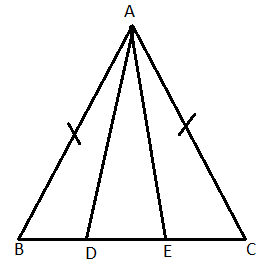
As we have an isosceles triangle ABC with AB = AC, where D and E are points on BC such that BE = CD and we need to prove that the sides AD and AE are equal i.e. AD = AE.
So, diagram can be given as

So, we have
AB = AC……………..(i)
BE = CD…………….(ii)
Now, we know the property of triangles that opposite angles of the opposite sides are equal if sides are equal. It means
And from equation (ii), we (iii) have BE = CD
Now, subtract DE from both sides of terms of the above equation. So, we get
BE – DE = CD – DE
Now, we can observe that the diagram is replaced by side BD and CD – DE by side CE. Hence, we get above equation as
BD = CE………………….(iv)
Now, in
AB = AC (from equation (i))
BD = CE (from equation (iv))
Hence,
So, now all the corresponding sides and angles of triangles ABD and ACE are equal by the C.P.C.T property of congruent triangles.
Hence, we get
AD = AE ( C.P.C.T)
So, it proved that AD and AE are equal.
Note: Another approach for proving AD = AE, we can prove the triangles ABE and ADE as congruent triangle in the following way:
AB = AC
BE = DC
By SAS criteria
Latest Vedantu courses for you
Grade 10 | MAHARASHTRABOARD | SCHOOL | English
Vedantu 10 Maharashtra Pro Lite (2025-26)
School Full course for MAHARASHTRABOARD students
₹33,300 per year
Recently Updated Pages
Master Class 10 General Knowledge: Engaging Questions & Answers for Success

Master Class 10 Computer Science: Engaging Questions & Answers for Success

Master Class 10 Science: Engaging Questions & Answers for Success

Master Class 10 Social Science: Engaging Questions & Answers for Success

Master Class 10 Maths: Engaging Questions & Answers for Success

Master Class 10 English: Engaging Questions & Answers for Success

Trending doubts
A boat goes 24 km upstream and 28 km downstream in class 10 maths CBSE

Why is there a time difference of about 5 hours between class 10 social science CBSE

The British separated Burma Myanmar from India in 1935 class 10 social science CBSE

The Equation xxx + 2 is Satisfied when x is Equal to Class 10 Maths

Chandigarh is the capital of A Punjab B Haryana C Punjab class 10 social science CBSE

Change the following sentences into negative and interrogative class 10 english CBSE




