Question

In an isosceles triangle, the vertex angle is twice of either of the base angles. Find the base and vertex angles. (Let the angle be b in degrees. Remember that the sum of angles of a triangle is \[{{180}^{\circ }}\])

Answer 1

Hint:- In this question, we first need to assume some variable for the base angle and then write the vertex angle in terms of the base angle. Now, using the conditions for angles in a triangle we can further simplify it to get the answer.

Complete step-by-step solution -

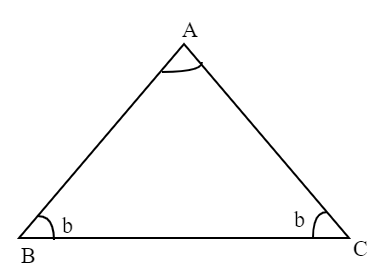
As we already know that the base angles in an isosceles triangle are equal.
Now, let us assume the base angle of the isosceles triangle as b.
Now, from the given condition that the vertex angle is twice the base angle we get,
 Vertex angle which is A \[=2b\]
Now, from the condition that the sum of angles in a triangle is \[{{180}^{\circ }}\].
Here A,B,C are the angles of the triangle. So we can write A+B+C = ${180}^{\circ}$
\[\Rightarrow b+b+2b={{180}^{\circ }}\]
Now, on further simplifying this we get,
\[\Rightarrow 4b={{180}^{\circ }}\]
Now, on dividing both sides with 4 we get,
\[\Rightarrow b=\dfrac{{{180}^{\circ }}}{4}\]
Now, on simplification of the above equation we get,
\[\therefore b={{45}^{\circ }}\]
Now, by substituting this value of b in the relation between the base angle and the vertex angle we get,
\[\begin{align}
  & \Rightarrow 2b=2\times {{45}^{\circ }} \\
 & \therefore 2b={{90}^{\circ }} \\
\end{align}\]
Hence, the base angle of the given isosceles triangle is \[{{45}^{\circ }}\] and the vertex angle is \[{{90}^{\circ }}\].

Note: It is important to note that the base angles in an isosceles triangle are equal. So, while considering the condition of the sum of the angles in a triangle as we know the relation between the base angle and the vertex angle now we get all the angles in terms of b and can get the value of b.
While calculating the value of b we need to be careful about rearranging the terms and on multiplying and dividing because neglecting any of the terms changes the result completely.