
In an orthorhombic crystal, a lattice plane cuts intercepts in the ratio 1:2:3 along a,b and c axes. Find the miller indices of the plane. Sketch the plane and calculate the interplanar spacing, given that a=1A, b=2A and c=3A.
Answer
488.4k+ views
1 likes
Hint: We have to calculate Miller indices by taking the reciprocals of intercepts and for calculating the interplanar spacing, we have to use the formula,
Here, h, k, and l are miller indices.
Complete step by step answer:
We know that the orthorhombic crystal system is one of the 7 crystal systems.
Orthorhombic lattices comes from enlarging a cubic lattice along two of its orthogonal pairs by two factors, that leads in a rectangular prism with a rectangular base (a by b) and height (c), such that a, b, and c are different.
The intersection of all three bases at 90° angles, so the three lattice vectors remain mutually orthogonal.
We know that Miller indices of a plane are the reciprocals of the intercepts of that corresponding to unit length.
Thus, intercepts are a:b:c=1:2:3.
So let us now take the reciprocals:
(or) We can take L.C.M and by taking L.C.M, we get the value of miller indices as 6,3,2.
The value of h is 6.
The value of k is 3.
The value of l is 2.
We can represent the miller indices as
Let us now calculate the interplanar spacing for orthorhombic crystals.
Let us now substitute the values of a, c, h, k, and l to calculate the interplanar spacing.
The inter-planar spacing is
The plane is sketched as,
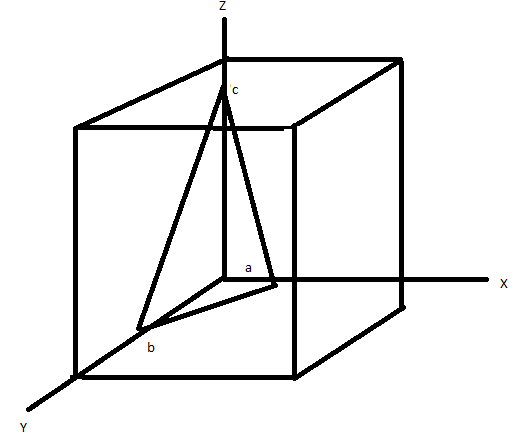
Note:
We have to know that in two dimensions there are two orthorhombic Bravais lattices: primitive rectangular and centered rectangular. In three dimensions, primitive orthorhombic, base-centered orthorhombic, body-centered orthorhombic, and face-centered orthorhombic are the four orthorhombic Bravais lattices.
Here, h, k, and l are miller indices.
Complete step by step answer:
We know that the orthorhombic crystal system is one of the 7 crystal systems.
Orthorhombic lattices comes from enlarging a cubic lattice along two of its orthogonal pairs by two factors, that leads in a rectangular prism with a rectangular base (a by b) and height (c), such that a, b, and c are different.
The intersection of all three bases at 90° angles, so the three lattice vectors remain mutually orthogonal.
We know that Miller indices of a plane are the reciprocals of the intercepts of that corresponding to unit length.
Thus, intercepts are a:b:c=1:2:3.
So let us now take the reciprocals:
(or) We can take L.C.M and by taking L.C.M, we get the value of miller indices as 6,3,2.
The value of h is 6.
The value of k is 3.
The value of l is 2.
We can represent the miller indices as
Let us now calculate the interplanar spacing for orthorhombic crystals.
Let us now substitute the values of a, c, h, k, and l to calculate the interplanar spacing.
The inter-planar spacing is
The plane is sketched as,

Note:
We have to know that in two dimensions there are two orthorhombic Bravais lattices: primitive rectangular and centered rectangular. In three dimensions, primitive orthorhombic, base-centered orthorhombic, body-centered orthorhombic, and face-centered orthorhombic are the four orthorhombic Bravais lattices.
Latest Vedantu courses for you
Grade 11 Science PCM | CBSE | SCHOOL | English
CBSE (2025-26)
School Full course for CBSE students
₹41,848 per year
Recently Updated Pages
Master Class 9 General Knowledge: Engaging Questions & Answers for Success

Master Class 9 English: Engaging Questions & Answers for Success

Master Class 9 Science: Engaging Questions & Answers for Success

Master Class 9 Social Science: Engaging Questions & Answers for Success

Master Class 9 Maths: Engaging Questions & Answers for Success

Class 9 Question and Answer - Your Ultimate Solutions Guide

Trending doubts
State and prove Bernoullis theorem class 11 physics CBSE

Who built the Grand Trunk Road AChandragupta Maurya class 11 social science CBSE

1 ton equals to A 100 kg B 1000 kg C 10 kg D 10000 class 11 physics CBSE

State the laws of reflection of light

One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

Difference Between Prokaryotic Cells and Eukaryotic Cells




