
In diammonium hydrogen phosphate, ${{(N{{H}_{4}})}_{2}}HP{{O}_{4}}$, the percentage of:
(This question has multiple correct options.)
(A) ${{P}_{2}}{{O}_{5}}$ is 53.78%
(B) $N{{H}_{3}}$ is 25.76%
(C) P is maximum
(D) N is minimum
Answer
523.8k+ views
Hint: To solve this question we first need to determine the molecular mass of diammonium hydrogen phosphate, ${{(N{{H}_{4}})}_{2}}HP{{O}_{4}}$. The molecular mass of one mole of a compound can be calculated by taking the sum of atomic masses of all the elements present in the molecule.
Complete answer:
Now, we know that the atomic mass of
N = 14.01 u
H = 1.010 u
P = 30.97 u
O = 16.00 u
Diammonium hydrogen phosphate, ${{(N{{H}_{4}})}_{2}}HP{{O}_{4}}$, can also be written as ${{H}_{9}}{{N}_{2}}{{O}_{4}}P$.
So, the molar mass of diammonium hydrogen phosphate (${{(N{{H}_{4}})}_{2}}HP{{O}_{4}}$) will be
\[\begin{align}
& {{M}_{{{(N{{H}_{4}})}_{2}}HP{{O}_{4}}}}=2\times {{M}_{N}}+9\times {{M}_{H}}+4\times {{M}_{O}}+{{M}_{P}} \\
& {{M}_{{{(N{{H}_{4}})}_{2}}HP{{O}_{4}}}}=2\times 14.01+9\times 1.01+4\times 16+30.97 \\
& {{M}_{{{(N{{H}_{4}})}_{2}}HP{{O}_{4}}}}=132.06\text{ g/mol} \\
\end{align}\]
Now, the formula to calculate the percentage composition of a constituent in a compound is given by:
\[%\text{ composition = }\dfrac{\text{mass of molecule in 1 mole of compound}}{\text{molar mass of compound}}\times 100\]
So, the percentage compositions of elements N, H, O, and P are as follows
\[\begin{align}
& (N)=\dfrac{2\times 14.01}{132.06}\times 100=21.21 \\
& (H)=\dfrac{9\times 1.01}{132.06}\times 100=6.87 \\
& (O)=\dfrac{4\times 16}{132.06}\times 100=48.46 \\
& (P)=\dfrac{30.97}{132.06}\times 100=23.45 \\
\end{align}\]
From the above calculations, we can see that the percentage compositions of elements in ${{(N{{H}_{4}})}_{2}}HP{{O}_{4}}$ are
N = 21.21%
H = 6.870%
O = 48.46%
P = 23.45 %
Now, diammonium hydrogen phosphate is produced as follows
\[{{P}_{2}}{{O}_{5}}+4N{{H}_{3}}+3{{H}_{2}}O\to 2{{(N{{H}_{4}})}_{2}}HP{{O}_{4}}\]
Hence, we can say that one mole of diammonium hydrogen phosphate (${{(N{{H}_{4}})}_{2}}HP{{O}_{4}}$) consists of a half mole of phosphorus pentoxide (${{P}_{2}}{{O}_{5}}$).
Also, it can be said that one mole of diammonium hydrogen phosphate (${{(N{{H}_{4}})}_{2}}HP{{O}_{4}}$) consists of two moles of ammonia ($N{{H}_{3}}$).
So, the percentage compositions of ${{P}_{2}}{{O}_{5}}$ and $N{{H}_{3}}$ will be
$\begin{align}
& ({{P}_{2}}{{O}_{5}})=\dfrac{0.5\times [2\times 30.97+5\times 16]}{132.06}\times 100=53.78 \\
& (N{{H}_{3}})=\dfrac{2\times [14.01+3\times 1.01]}{132.06}\times 100=25.76 \\
\end{align}$
From the above calculations, we can see that the percentage compositions of ${{P}_{2}}{{O}_{5}}$ and $N{{H}_{3}}$ in ${{(N{{H}_{4}})}_{2}}HP{{O}_{4}}$ are
${{P}_{2}}{{O}_{5}}$ = 53.78%
$N{{H}_{3}}$ = 25.76%
So, the correct answers are option (A) and option (B).
Note:
It should be noted that upon dissociation at a temperature of $100{}^\circ C$ and dissociation pressure of 5mmHg, diammonium hydrogen phosphate dissociates as follows
\[{{(N{{H}_{4}})}_{2}}HP{{O}_{4}}(s)\rightleftarrows N{{H}_{3}}(g)+(N{{H}_{4}}){{H}_{2}}P{{O}_{4}}(s)\]
The structure of diammonium hydrogen phosphate salt is as follows.
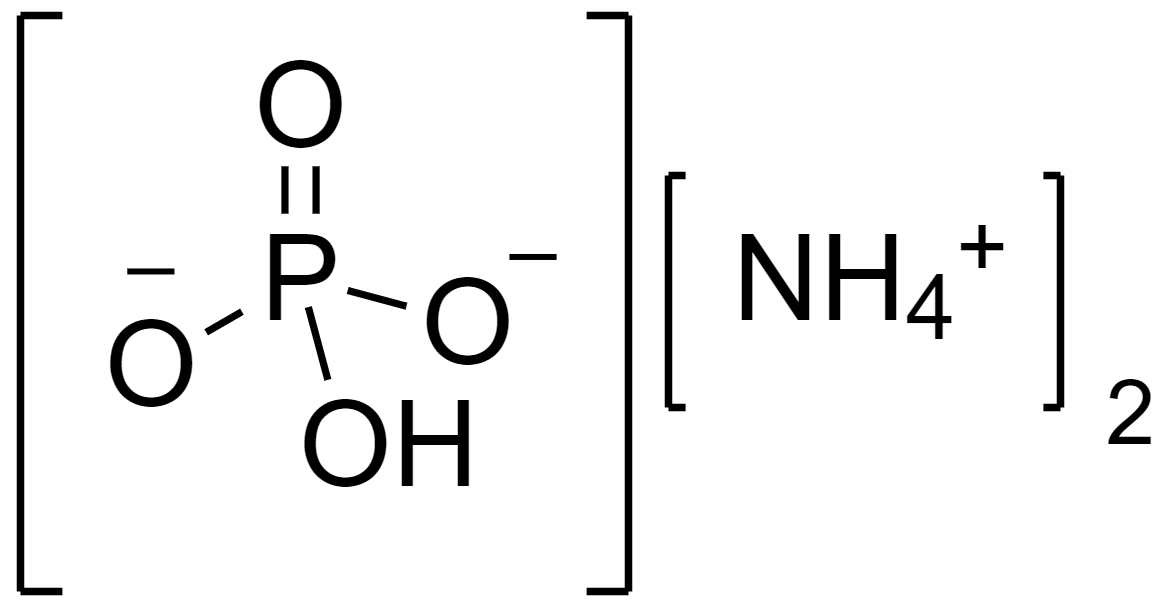
Complete answer:
Now, we know that the atomic mass of
N = 14.01 u
H = 1.010 u
P = 30.97 u
O = 16.00 u
Diammonium hydrogen phosphate, ${{(N{{H}_{4}})}_{2}}HP{{O}_{4}}$, can also be written as ${{H}_{9}}{{N}_{2}}{{O}_{4}}P$.
So, the molar mass of diammonium hydrogen phosphate (${{(N{{H}_{4}})}_{2}}HP{{O}_{4}}$) will be
\[\begin{align}
& {{M}_{{{(N{{H}_{4}})}_{2}}HP{{O}_{4}}}}=2\times {{M}_{N}}+9\times {{M}_{H}}+4\times {{M}_{O}}+{{M}_{P}} \\
& {{M}_{{{(N{{H}_{4}})}_{2}}HP{{O}_{4}}}}=2\times 14.01+9\times 1.01+4\times 16+30.97 \\
& {{M}_{{{(N{{H}_{4}})}_{2}}HP{{O}_{4}}}}=132.06\text{ g/mol} \\
\end{align}\]
Now, the formula to calculate the percentage composition of a constituent in a compound is given by:
\[%\text{ composition = }\dfrac{\text{mass of molecule in 1 mole of compound}}{\text{molar mass of compound}}\times 100\]
So, the percentage compositions of elements N, H, O, and P are as follows
\[\begin{align}
& (N)=\dfrac{2\times 14.01}{132.06}\times 100=21.21 \\
& (H)=\dfrac{9\times 1.01}{132.06}\times 100=6.87 \\
& (O)=\dfrac{4\times 16}{132.06}\times 100=48.46 \\
& (P)=\dfrac{30.97}{132.06}\times 100=23.45 \\
\end{align}\]
From the above calculations, we can see that the percentage compositions of elements in ${{(N{{H}_{4}})}_{2}}HP{{O}_{4}}$ are
N = 21.21%
H = 6.870%
O = 48.46%
P = 23.45 %
Now, diammonium hydrogen phosphate is produced as follows
\[{{P}_{2}}{{O}_{5}}+4N{{H}_{3}}+3{{H}_{2}}O\to 2{{(N{{H}_{4}})}_{2}}HP{{O}_{4}}\]
Hence, we can say that one mole of diammonium hydrogen phosphate (${{(N{{H}_{4}})}_{2}}HP{{O}_{4}}$) consists of a half mole of phosphorus pentoxide (${{P}_{2}}{{O}_{5}}$).
Also, it can be said that one mole of diammonium hydrogen phosphate (${{(N{{H}_{4}})}_{2}}HP{{O}_{4}}$) consists of two moles of ammonia ($N{{H}_{3}}$).
So, the percentage compositions of ${{P}_{2}}{{O}_{5}}$ and $N{{H}_{3}}$ will be
$\begin{align}
& ({{P}_{2}}{{O}_{5}})=\dfrac{0.5\times [2\times 30.97+5\times 16]}{132.06}\times 100=53.78 \\
& (N{{H}_{3}})=\dfrac{2\times [14.01+3\times 1.01]}{132.06}\times 100=25.76 \\
\end{align}$
From the above calculations, we can see that the percentage compositions of ${{P}_{2}}{{O}_{5}}$ and $N{{H}_{3}}$ in ${{(N{{H}_{4}})}_{2}}HP{{O}_{4}}$ are
${{P}_{2}}{{O}_{5}}$ = 53.78%
$N{{H}_{3}}$ = 25.76%
So, the correct answers are option (A) and option (B).
Note:
It should be noted that upon dissociation at a temperature of $100{}^\circ C$ and dissociation pressure of 5mmHg, diammonium hydrogen phosphate dissociates as follows
\[{{(N{{H}_{4}})}_{2}}HP{{O}_{4}}(s)\rightleftarrows N{{H}_{3}}(g)+(N{{H}_{4}}){{H}_{2}}P{{O}_{4}}(s)\]
The structure of diammonium hydrogen phosphate salt is as follows.

Recently Updated Pages
The number of solutions in x in 02pi for which sqrt class 12 maths CBSE

Write any two methods of preparation of phenol Give class 12 chemistry CBSE

Differentiate between action potential and resting class 12 biology CBSE

Two plane mirrors arranged at right angles to each class 12 physics CBSE

Which of the following molecules is are chiral A I class 12 chemistry CBSE

Name different types of neurons and give one function class 12 biology CBSE

Trending doubts
One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

Explain zero factorial class 11 maths CBSE

What is 1s 2s 2p 3s 3p class 11 chemistry CBSE

Discuss the various forms of bacteria class 11 biology CBSE

State the laws of reflection of light

An example of chemosynthetic bacteria is A E coli B class 11 biology CBSE




