
In elliptical orbit of a planet, as the planet moves from the apogee position to the perigee position:
Column-I Column-II (a) Speed of planet (p) Remains same (b) Distance of planet from centre of Sun (q) Decreases (c) Potential energy (r) Increases (d) Angular Momentum about centre of Sun (s) Cannot say
A). (a-p), (b-q), (c-r), (d-s)
B). (a-s), (b-r), (c-p), (d-q)
C). (a-r), (b-q), (c-q), (d-p)
D). None of these
| Column-I | Column-II |
| (a) Speed of planet | (p) Remains same |
| (b) Distance of planet from centre of Sun | (q) Decreases |
| (c) Potential energy | (r) Increases |
| (d) Angular Momentum about centre of Sun | (s) Cannot say |
Answer
542.4k+ views
Hint: Recall Kepler’s Laws to deduce the variation in the planet’s speed as it traverses from the apogee to the perigee. Then use the definition of apogee and perigee to determine how the distance between the planet and the Sun would change in such a motion. Then, keeping in mind that the potential energy between the Sun and the planet is due to an attractive potential that is dependent on the distance between the two, find the variance of potential energy. To this end, use Kepler’s Laws and your previous deductions to determine the nature of variation of angular momentum about the orbital focus.
Formula Used:
Kepler’s Third Law: $T^2 \propto R^3$
Gravitational potential energy: $U = -\dfrac{GMm}{R}$
Complete step-by-step solution:
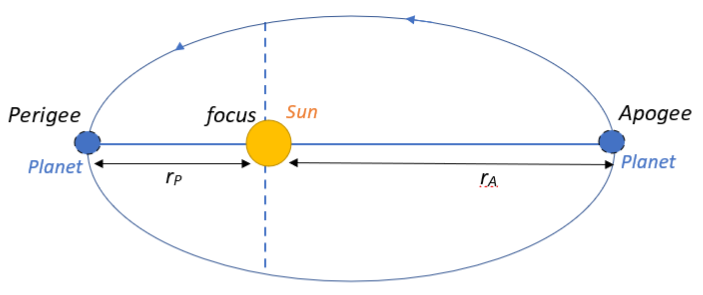
We are given that a planet executes an elliptical orbit around the Sun, as shown in the figure. This means that the Sun is located at the focus of the elliptical orbit. We will now look at the dynamics of such motion as the planet traverses from the apogee position to the perigee position.
Apogee is the point on the elliptical orbit that is at the farthest distance from the focus, whereas perigee is the point on the elliptical orbit that is closest to the focus. Keeping this in mind, let us look at the given parameters and their variance as the planet progresses from the apogee to the perigee.
a). Speed of the planet
From Kepler’s Third Law which states that the ratio of the square of the orbital period$\;t$ of a planet and the cube of its distance$\;r$ from the focus of its orbit is constant, say k, for all planets, we have:
$\dfrac{t^2}{r^3} = k \Rightarrow t^2 = kr^3 \Rightarrow t^2 \propto r^3$
Let the distance between the planet and the sun at the apogee and perigee be $r_A$ and $r_P$ respectively.
Clearly $r_P < r_A$,
So as the planet moves from apogee to perigee, the distance between the planet and the Sun decreases.
Since $t^2 \propto r^3$,
the time taken to traverse through the apogee and perigee positions will be related as:
$t_P < t_A$, which means that the time decreases.
Since the speed of the planet is inversely proportional to the time it takes to traverse the orbit, the speed of the planet as it moves from the apogee to the perigee will increase.
Therefore, (a) Speed of the planet – (r) increases.
b). Distance of planet from centre of Sun
We know that as the planet traverses from the apogee to the perigee, i.e., from the farthest point in orbit to the closest point in orbit from the focus, which in our case is the Sun, the distance of the planet from the centre of the Sun decreases.
Therefore, (b) Distance of the planet from the centre of the Sun - (q) decreases.
c). Potential energy
The potential energy arising from an attractive gravitational force between the Sun and the planet can be given as:
$U = -\dfrac{GMm}{r} \Rightarrow U \propto -\dfrac{1}{r}$,
where$\;G$ is the gravitational constant,$\;M$ is the mass of the Sun, $\;m$ is the mass of the planet,$\;r$ is the distance between the Sun and the planet, and the negative sign indicates an attractive potential.
Now, we know that the distance$\;r$ between the Sun and the planet decreases as the planet moves from the apogee to the perigee. So, from the above relation, we see that the potential energy also decreases since we account for the negative sign.
Therefore, (c) Potential energy – (q) decreases.
d). Angular momentum about the centre of Sun
We saw that as the planet moves from the apogee to the perigee it speeds up, i.e., when$\;r$ decreases, $\;v$ increases in order to maintain the same rate at which the planet sweeps across the orbit, which is nothing but a way to conserve angular momentum. This is also given by Kepler’s Second Law which states that the radius between the Sun and the planet sweeps out equal areas in equal intervals of time, conserving angular momentum.
Therefore, (d) Angular momentum about the centre of Sun – (p) is conserved.
To this end, the correct choice would be C. (a-r), (b-q), (c-q), (d-p).
Note: It is important to understand that the angular momentum of the above elliptical system is conserved only when there is no net torque acting on the constituents of the system. Though gravity acts between the Sun and the planet, it does not contribute to any torque because the gravitational force points towards the Sun at the focus, which is the point around which the rotation occurs but the point, by itself, remains stationary. This means that we can apply the principle of conservation of angular momentum to our system since angular momentum is conserved at all points on the orbit and no other influencing forces are incident on it.
Formula Used:
Kepler’s Third Law: $T^2 \propto R^3$
Gravitational potential energy: $U = -\dfrac{GMm}{R}$
Complete step-by-step solution:
We are given that a planet executes an elliptical orbit around the Sun, as shown in the figure. This means that the Sun is located at the focus of the elliptical orbit. We will now look at the dynamics of such motion as the planet traverses from the apogee position to the perigee position.
Apogee is the point on the elliptical orbit that is at the farthest distance from the focus, whereas perigee is the point on the elliptical orbit that is closest to the focus. Keeping this in mind, let us look at the given parameters and their variance as the planet progresses from the apogee to the perigee.

a). Speed of the planet
From Kepler’s Third Law which states that the ratio of the square of the orbital period$\;t$ of a planet and the cube of its distance$\;r$ from the focus of its orbit is constant, say k, for all planets, we have:
$\dfrac{t^2}{r^3} = k \Rightarrow t^2 = kr^3 \Rightarrow t^2 \propto r^3$
Let the distance between the planet and the sun at the apogee and perigee be $r_A$ and $r_P$ respectively.
Clearly $r_P < r_A$,
So as the planet moves from apogee to perigee, the distance between the planet and the Sun decreases.
Since $t^2 \propto r^3$,
the time taken to traverse through the apogee and perigee positions will be related as:
$t_P < t_A$, which means that the time decreases.
Since the speed of the planet is inversely proportional to the time it takes to traverse the orbit, the speed of the planet as it moves from the apogee to the perigee will increase.
Therefore, (a) Speed of the planet – (r) increases.
b). Distance of planet from centre of Sun
We know that as the planet traverses from the apogee to the perigee, i.e., from the farthest point in orbit to the closest point in orbit from the focus, which in our case is the Sun, the distance of the planet from the centre of the Sun decreases.
Therefore, (b) Distance of the planet from the centre of the Sun - (q) decreases.
c). Potential energy
The potential energy arising from an attractive gravitational force between the Sun and the planet can be given as:
$U = -\dfrac{GMm}{r} \Rightarrow U \propto -\dfrac{1}{r}$,
where$\;G$ is the gravitational constant,$\;M$ is the mass of the Sun, $\;m$ is the mass of the planet,$\;r$ is the distance between the Sun and the planet, and the negative sign indicates an attractive potential.
Now, we know that the distance$\;r$ between the Sun and the planet decreases as the planet moves from the apogee to the perigee. So, from the above relation, we see that the potential energy also decreases since we account for the negative sign.
Therefore, (c) Potential energy – (q) decreases.
d). Angular momentum about the centre of Sun
We saw that as the planet moves from the apogee to the perigee it speeds up, i.e., when$\;r$ decreases, $\;v$ increases in order to maintain the same rate at which the planet sweeps across the orbit, which is nothing but a way to conserve angular momentum. This is also given by Kepler’s Second Law which states that the radius between the Sun and the planet sweeps out equal areas in equal intervals of time, conserving angular momentum.
Therefore, (d) Angular momentum about the centre of Sun – (p) is conserved.
To this end, the correct choice would be C. (a-r), (b-q), (c-q), (d-p).
Note: It is important to understand that the angular momentum of the above elliptical system is conserved only when there is no net torque acting on the constituents of the system. Though gravity acts between the Sun and the planet, it does not contribute to any torque because the gravitational force points towards the Sun at the focus, which is the point around which the rotation occurs but the point, by itself, remains stationary. This means that we can apply the principle of conservation of angular momentum to our system since angular momentum is conserved at all points on the orbit and no other influencing forces are incident on it.
Recently Updated Pages
Master Class 11 Computer Science: Engaging Questions & Answers for Success

Master Class 11 Business Studies: Engaging Questions & Answers for Success

Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 English: Engaging Questions & Answers for Success

Master Class 11 Maths: Engaging Questions & Answers for Success

Master Class 11 Biology: Engaging Questions & Answers for Success

Trending doubts
One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

There are 720 permutations of the digits 1 2 3 4 5 class 11 maths CBSE

Discuss the various forms of bacteria class 11 biology CBSE

Draw a diagram of a plant cell and label at least eight class 11 biology CBSE

State the laws of reflection of light

Explain zero factorial class 11 maths CBSE




