Question

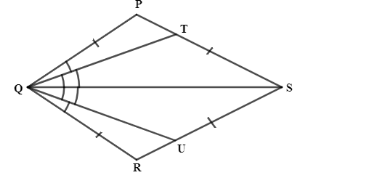
In fig. PQRS is a quadrilateral and T and U are respectively points on PS and RS such that
$PQ=RQ$
$\angle PQT=\angle RQU$ ………………………(i)
$\angle TQS=\angle UQS$ ………………………(ii)
Prove that $QT=QU$.

Answer 1

Hint: First of all, we will find the sum of angles of a quadrilateral and then using that we will find the triangles which are equivalent to each other. Then using the laws of triangles which is given as when two sides and one angle of two triangles are the same i.e. side angle side rule (SAS), then those two triangles are equivalent to each other. By using this, we will prove $QT=QU$.

Complete step-by-step answer:
Now, in question we are given that, $\angle PQT=\angle RQU$ and $\angle TQS=\angle UQS$, which can be written as,
$\angle PQT=\angle RQU$ ……………..(i)
$\angle TQS=\angle UQS$ ……………….(ii)

Now, on adding the terms of expression (i) and (ii) we will get,
$\begin{align}
  & \angle PQT=\angle RQU \\
 & +\angle TQS=\angle UQS \\
\end{align}$
$\Rightarrow \angle PQT+\angle TQS=\angle RQU+\angle UQS$ …………….(iii)
Now, from the figure it can be seen that ,
$\angle PQS=\angle PQT+\angle TQS$ ………………..(iv)
And $\angle SQR=\angle RQU+\angle UQS$ …………..(v)
Now, substituting the values of equation (iv) and (v) in expression (iii), we will get,
$\angle PQS=\angle SQR$ ………………..(vi)
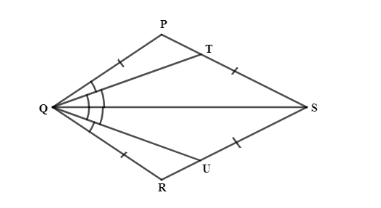
Now, we can see that there are two triangles in the quadrilateral PQRS, which are,
$\Delta PQS$ and $\Delta RQS$
Now, in $\Delta PQS$ and $\Delta RQS$, two sides are common which can be given as,
$PQ=RQ$
And two angles are equal which we found in expression (iv) i.e. $\angle PQS=\angle SQR$
We are also given that $PQ=RQ$, using all these relations we can say that it satisfies the side angle side rule of triangle, which states that when two sides and one angle of two triangles are same then those two triangles are equivalent to each other, this can be written mathematically as,
$\Delta PQS\cong \Delta RQS$
Now, as two triangles of a quadrilateral are equivalent to each other, two opposite angles will also be equal, which can be given as,
$\angle QPS=\angle QRS$
Now, on observing the figure it can be seen that $\angle P$ is a common angle in $\angle QPS$ and $\angle QPT$, in the same way $\angle R$ is a common angle in $\angle QRS$ and $\angle QRU$. So, from this we can say that $\angle QPT=\angle QRU$ ……………………..(vii)
Now, in $\Delta PQS$ and $\Delta RQS$, we are given that,
Two sides are same i.e. $QP=QR$
And two angles are equal which we found in expression (ii) i.e. $\angle PQT=\angle QRU$ ,
We are also given that $\angle PQT=\angle RQU$
So, from all these relations we can say that it satisfies the angle side angle theorem, which states that in triangle when, two angles and one side are common then those two triangles are equivalent to them, which can be given mathematically as,
$\Delta QPT\cong \Delta QRS$
Now, as two triangles of a quadrilateral are equivalent to each other, two opposite sides will also be equal, which can be given as,
$QT=QU$
Hence, proved as given in the question.

Note: In such a type of question, students might make mistakes in considering the same angle and same sides of the triangle and they might get confused in considering the equivalency of the triangles and due to that the sum might get wrong results, students must be careful in selecting corresponding sides of the two triangles equivalent to each other..