Question

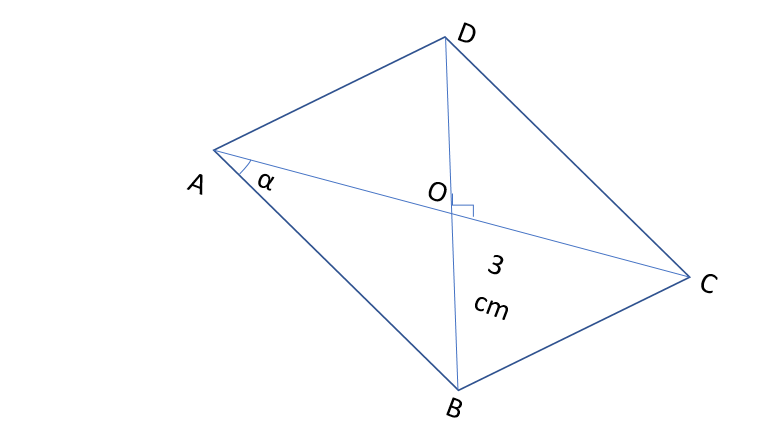
In figure ABCD is a rhombus whose diagonals AC makes an angle alpha with AB. If \[\cos \alpha = \dfrac{2}{3}\] and OB = 3 cm, Find the lengths of diagonals AC and BD.

Answer 1

Hint: In a right triangle, the square of the hypotenuse is equal to the sum of the squares of the other two sides.
\[{a^2} = {b^2} + {c^2}\]
Use Pythagorean Theorem to solve the problem.

Complete step by step solution:
In figure ABCD is a rhombus \[\cos \alpha = \dfrac{2}{3}\] and OB = 3 cm
\[\vartriangle AOB,\;\vartriangle BOC,\;\vartriangle COD\;and\;\vartriangle AOD\]are right triangles
In \[\vartriangle AOB\], \[\cos \alpha = \dfrac{2}{3} = \dfrac{{AO}}{{AB}}\]
As per the above equation and taking x as a variable in the above equation, we can say
\[OA = 2x\] and \[AB = 3x\]
In \[\vartriangle AOB\]which is a right angles triangle by applying Pythagoras theorem:-
\[ \Rightarrow A{B^2} = A{O^2} + B{O^2}\]
\[ \Rightarrow {\left( {3x} \right)^2} = {\left( {2x} \right)^2} + {3^2}\]
We will first try to convert the above equation into standard form of a quadratic equation
\[ \Rightarrow 9{x^2} = 4{x^2} + 9\]
Now we will try to isolate the x terms in the equation.
\[ \Rightarrow 9{x^2} - 4{x^2} = 9\]
\[ \Rightarrow 5{x^2} = 9\]
\[ \Rightarrow {x^2} = \dfrac{9}{5}\]
When I'm solving an equation, I know that I can do whatever I like to that equation as long as I do the exact same thing to both sides of that equation. On the left-hand side of this particular equation, I have an x2, and I want a plain old x. To turn the x2 into an x, I can take the square root of each side of the equation, like this:
\[ \Rightarrow x = \sqrt {\dfrac{9}{5}} \]
\[ \Rightarrow x = \dfrac{3}{{\sqrt 5 }}\]
\[
  Hence,\;OA\; = 2x = 2{\times}\dfrac{3}{{\sqrt 5 }} = \dfrac{6}{{\sqrt 5 }}cm \\
  and\;AB = 3x = 3{\times}\dfrac{3}{{\sqrt 5 }} = \dfrac{9}{{\sqrt 5 }}cm \\
 \]
\[
  Hence\;diagonal \\
  BD = 2{\times}OB = 2{\times}3 = 6\;cm \\
  AC = 2{\times }OA = 2{\times}\dfrac{6}{{\sqrt 5 }} = \dfrac{{12}}{{\sqrt 5 }}cm \\
 \]

The length of diagonals AC=$\dfrac{{12}}{{\sqrt 5 }}cm$ and BD=$6$cm .

Note:
The general approach is to collect all ${x^2}$ terms on one side of the equation while keeping the constants to the opposite side. After doing so, the next obvious step is to take the square roots of both sides to solve for the value of x. Always attach the symbol $ \pm $ when you get the square root of the constant.