Question

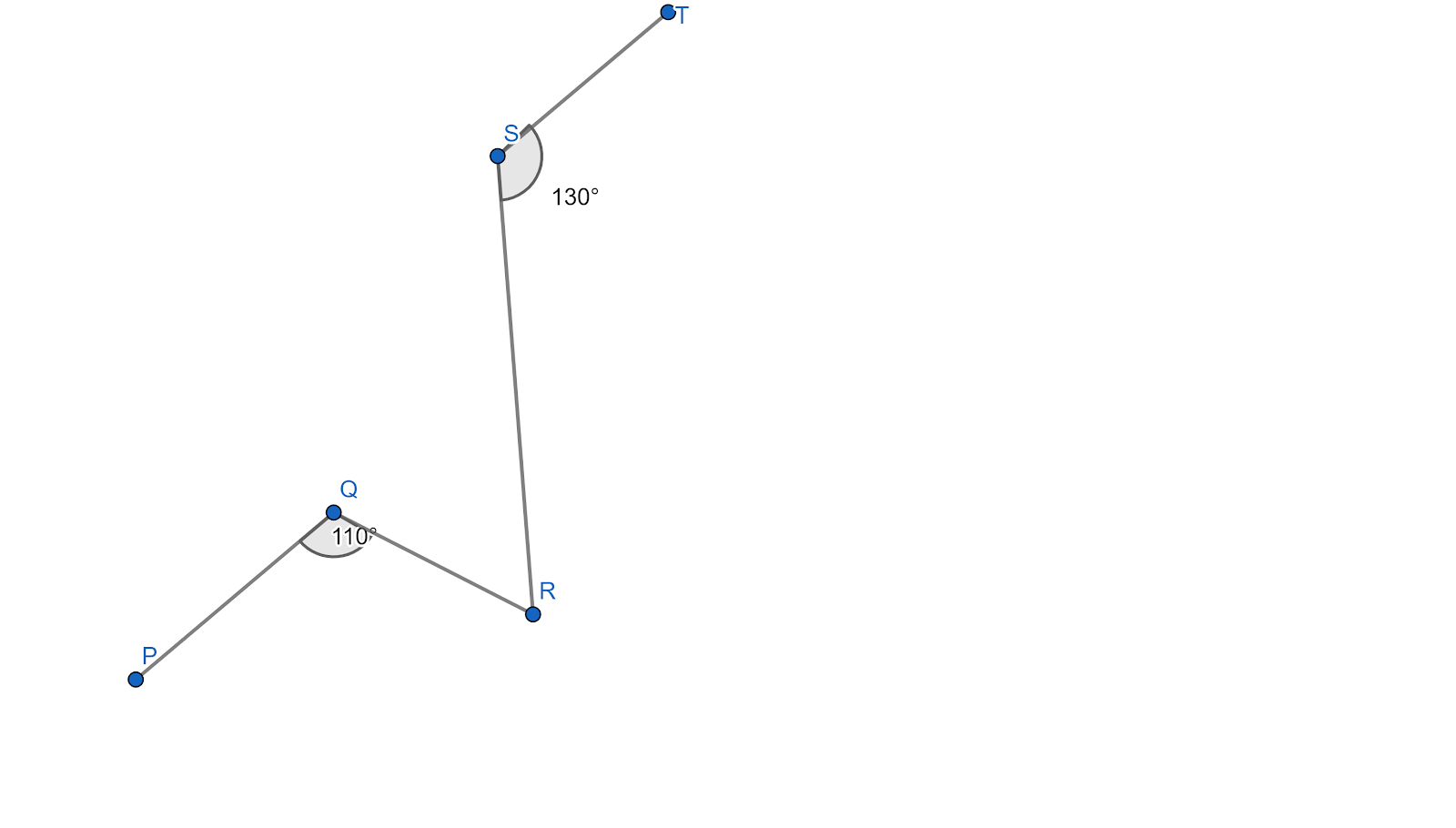
In given figure, if$PQ||ST$, $\angle PQR={{110}^{\circ }}$ and$\angle RST={{130}^{\circ }}$, Find$\angle QRS$.

Answer 1

Hint: For our convenience and to make the question simply we will draw a line parallel to $ST$ through point$R$. And extend the lines $PQ$ and $ST$and identify the corresponding and alternative interior and alternative exterior angles and use the transversal law and exterior angle rule for a triangle.
From the concept, we know that the transversal law states that corresponding angles are congruent and interior angles on the same side of the transversal are supplementary and alternative interior angles are also congruent.
From the concept, we also know that the exterior angle rule of a triangle states that the measure of an exterior angle of a triangle is equal to the sum of two opposite interior angles in that triangle.

Complete step by step answer:
Given in the question that,$PQ||ST$, $\angle PQR={{110}^{\circ }}$ and$\angle RST={{130}^{\circ }}$
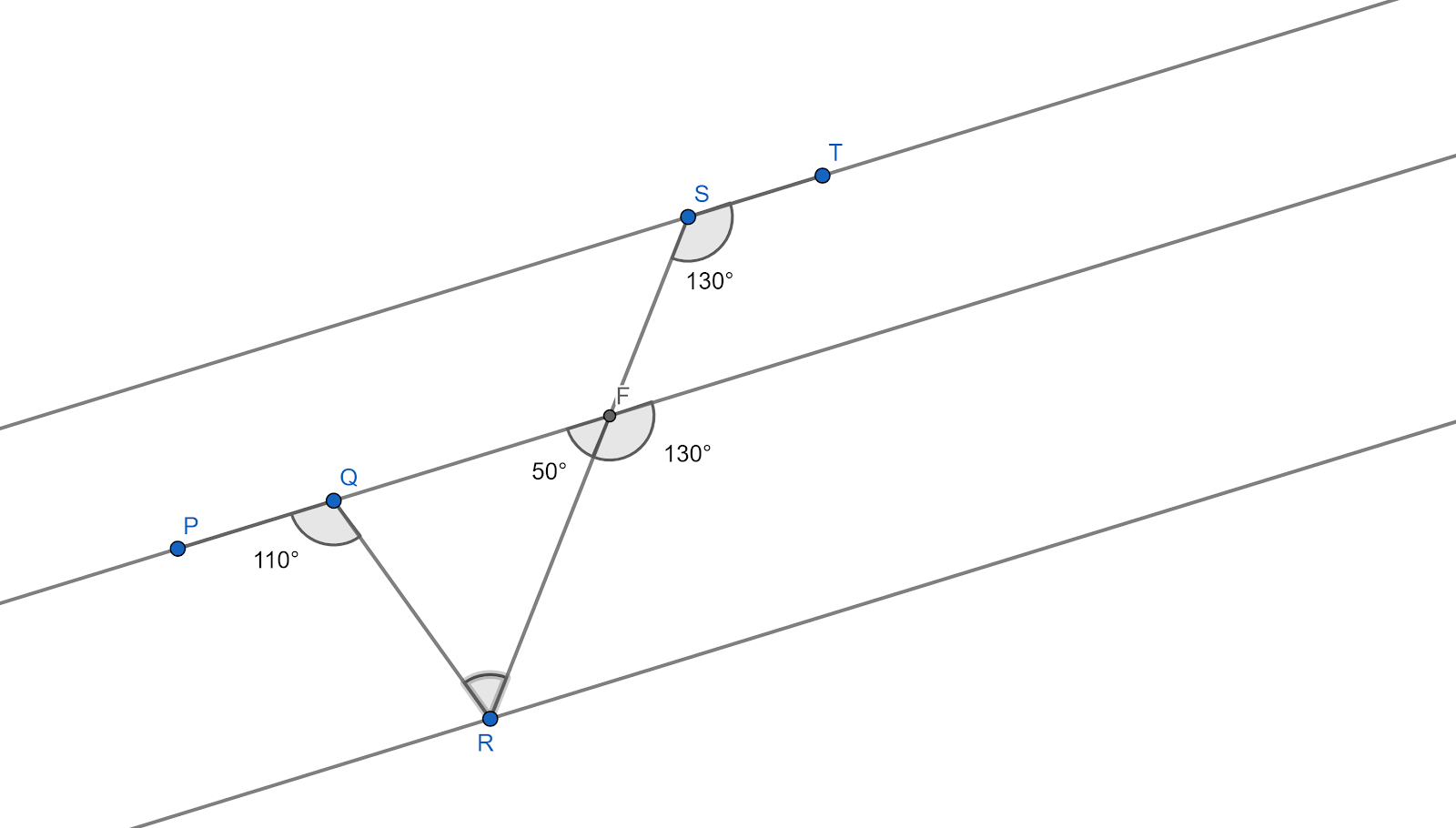
Let us extend $PQ$ and $ST$and draw a line parallel to $ST$ through point$R$.
Let the meeting point of $SR$ and the extension of $PQ$ be$O$.

From the concept, we know that the transversal law states that corresponding angles are congruent and interior angles on the same side of the transversal are supplementary and alternative interior angles are also congruent.
From the law of transversal $\angle QOR={{50}^{\circ }}$
Here if we observe carefully there is a $\vartriangle QOR$formed.
From the concept, we know that the exterior angle rule of a triangle says that the measure of an exterior angle of a triangle is equal to the sum of two opposite interior angles in that triangle.
From the exterior angle rule of a triangle,
 $\begin{align}
  & \angle QRO+\angle QOR=\angle PQR \\
 & \Rightarrow \angle QRO+{{50}^{\circ }}={{110}^{\circ }} \\
 & \Rightarrow \angle QRO={{60}^{\circ }} \\
\end{align}$
Hence, $\angle QRS={{60}^{\circ }}$
Note:
 While solving questions of this type we should take care of the angles that we assume to be corresponding and the angles that are alternative interior and alternative exterior and the exterior angle of the triangle and it’s opposite 2 interior angles.