
In gravity free space iron man of mass ‘
a.
b.
c.
d.
Answer
483k+ views
Hint: According to the law of conservation of momentum, in an isolated system, the vector sum of linear momentum of all the bodies of the system is conserved and is not affected due to their mutual action or reaction. An isolated system means a system with no external force acting on it.
Complete step by step answer:
In the gravity-free space, there are no particles present in that system. Thus, there is no force acting on the iron man. For a system, the center of mass remains the same if there are no external forces on the system, that is, internal forces cannot change the center of mass of the system.
So we have to say that the net change in the center of
It is stated in a question, in a gravity-free space, a man of mass
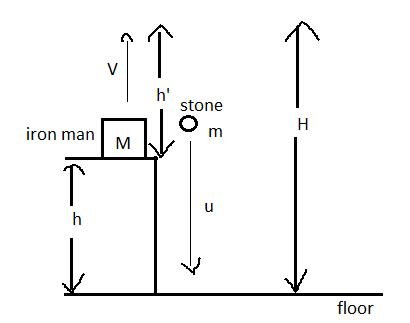
From the law of conservation of momentum,
We have to equate the terms we get,
Take
Here,
Now, time taken by the stone to reach floor is given by,
In that time, the height reached by the iron man of mass m is given by,
From the equation
So we can write it as equate form, we get
Let us take a cross-multiplication we get,
Take
The height reached by the man after releasing the stone from height is given by,
Substitute equation
Cancel the same terms we get,
Now we have to find out the total height,
The total height from the floor is given by,
Substitute equation
Taking
Hence, the correct answer is option (A).
Note: Momentum is a property of a moving body, which is a product of mass and velocity. The law of conservation of linear momentum is universal that as it applies to both, microscopic as well as macroscopic systems.
Complete step by step answer:
In the gravity-free space, there are no particles present in that system. Thus, there is no force acting on the iron man. For a system, the center of mass remains the same if there are no external forces on the system, that is, internal forces cannot change the center of mass of the system.
So we have to say that the net change in the center of
It is stated in a question, in a gravity-free space, a man of mass

From the law of conservation of momentum,
We have to equate the terms we get,
Take
Here,
Now, time taken by the stone to reach floor is given by,
In that time, the height reached by the iron man of mass m is given by,
From the equation
So we can write it as equate form, we get
Let us take a cross-multiplication we get,
Take
The height reached by the man after releasing the stone from height is given by,
Substitute equation
Cancel the same terms we get,
Now we have to find out the total height,
The total height from the floor is given by,
Substitute equation
Taking
Hence, the correct answer is option (A).
Note: Momentum is a property of a moving body, which is a product of mass and velocity. The law of conservation of linear momentum is universal that as it applies to both, microscopic as well as macroscopic systems.
Recently Updated Pages
Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 Business Studies: Engaging Questions & Answers for Success

Master Class 11 Accountancy: Engaging Questions & Answers for Success

Master Class 11 English: Engaging Questions & Answers for Success

Master Class 11 Computer Science: Engaging Questions & Answers for Success

Master Class 11 Maths: Engaging Questions & Answers for Success

Trending doubts
Which one is a true fish A Jellyfish B Starfish C Dogfish class 11 biology CBSE

State and prove Bernoullis theorem class 11 physics CBSE

1 ton equals to A 100 kg B 1000 kg C 10 kg D 10000 class 11 physics CBSE

In which part of the body the blood is purified oxygenation class 11 biology CBSE

One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

Difference Between Prokaryotic Cells and Eukaryotic Cells




