Question

In how many ways can a person go from point $A$ to point $B$ if he can travel only to the right or upward along the lines (Grid Problem)?

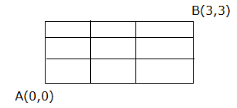
$A) 10$
$B) 20$
$C) 1$
$D) 16$

Answer 1

Hint: In this type of problem we need to find the ways from the point $A$ to point $B$ in the given figure by using the method of grid problem.
Here we have to use the formula for combination to solve this question.
Let us do some simplification, we get the required answer.

Formula used: ${}^n{C_r} = \dfrac{{n!}}{{r!(n - r)!}}$$ = \dfrac{{n(n - 1)(n - 2)(n - 3).....(n - (n - 1)!}}{{r(r - 1)(r - 2).....(r - (r - 1))!n(n - 1)(n - 2)........(n - (n - 1))!}}$

Complete step-by-step answer:
In the given figure below

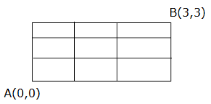
This is slightly different from the usual approach, to reach $(3,3)$to $(0,0)$we have to go $3$steps right $\left( R \right)$ and $3$ steps upwards $\left( U \right)$ in any order.
The number of possible arrangements of $3$$R's$ and $3$$U's$ will give the number of different paths.
The number of arrangements is given by ${}^6{C_3}$
Here\[\;n = 6\] and \[r = 3\] by using the formula ${}^n{C_r} = \dfrac{{n!}}{{r!(n - r)!}}$ we get,
Now let us expand the above expression by using the formula of combination $ = \dfrac{{6 \times 5 \times 4 \times 3!}}{{3! \times 3 \times 2 \times 1}}$
On cancellation of terms in the numerator and denominator we get,
We can have, $ = 5 \times 4$
Now we are multiplying the remaining terms $ = 20$
(As the $3$ $R's$ and $U's$ are identical)
Hence, we get the required number of ways are $20$ which is in the option of $(B)$

Hence, we get the number of ways a person can go from point $A$ to point $B$ if he can travel only to the right or upwards along the line.

Note: In general, permutation can be defined as the act of arranging all the members of a group in an order or sequence. We can also say that if the group is already arranged, then rearranging of the members is known as the procedure of permuting.
Combination can be defined as the technique of selecting things from a collection in such a manner that the order of selection does not matter. It is generally used where the order of data does not matter.