Question

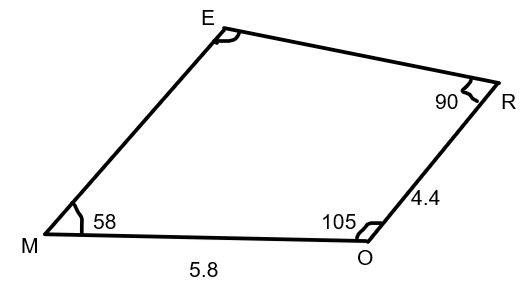
In quadrilateral MORE, $l$ (MO)$=5.8cm$, $l$(OR)$=4.4cm$, $\angle M={{58}^{\circ }},\angle O = {{105}^{\circ }},\angle R={{90}^{\circ }}$, any side can be base. Find the fourth angle.

Answer 1

Hint: Type of question is based on the properties of quadrilateral. As we had given three angles of figure and want to know the fourth angle. As by the angle sum property of a quadrilateral we know that the sum of all angles of a quadrilateral is ${{360}^{\circ }}$.

Complete step-by-step solution:
Moving ahead with the question, as we want to know the fourth angle of the quadrilateral i.e. named as $\angle E$. We know that the sum of all the angles of a quadrilateral is ${{360}^{\circ }}$. So we can write it as;
$\angle M+\angle O+\angle R+\angle E={{360}^{\circ }}$
By the given condition of question we know that$\angle M={{58}^{\circ }},\angle O={{105}^{\circ }},\angle R={{90}^{\circ }}$; put this value in above equation, then we will get;
$\begin{align}
  & \angle M+\angle O+\angle R+\angle E={{360}^{\circ }} \\
 &\Rightarrow {{58}^{\circ }}+{{105}^{\circ }}+{{90}^{\circ }}+\angle E={{360}^{\circ }} \\
\end{align}$
On solving it further, we will get;
$\begin{align}
  & {{58}^{\circ }}+{{105}^{\circ }}+{{90}^{\circ }}+\angle E={{360}^{\circ }} \\
 &\Rightarrow {{253}^{\circ }}+\angle E={{360}^{\circ }} \\
 &\Rightarrow \angle E={{360}^{\circ }}-{{253}^{\circ }} \\
 &\Rightarrow \angle E={{107}^{\circ }} \\
\end{align}$
From here we can say that fourth angle we got is ${{107}^{\circ }}$i.e. $\angle E={{107}^{\circ }}$
Hence answer is ${{107}^{\circ }}$.

Note: It is not mandatory that whatever data is given in the question must be used by us or required, it can be or it cannot be, it depends on what is asked. As we had in our question, we had no use of the given length of sides of quadrilateral.