Question

In square $ABCD$;$A = (3,4)$, $B = ( - 2,4)$, and $C = ( - 2, - 1)$ By plotting these points on a graph paper, find the area of the square.

Answer 1

Hint: First we have to plot the given points into a graph. Because we must know the distance between all the four pairs of points. Then we will start with the use of the distance formula to find the distance between all the four pairs of the points. After calculating the vertex of the point $D$ then we will find the area of the square $ABCD$.

Formula used: Distance between points formula $D = \sqrt {{{({x_2} - {x_1})}^2} + {{({y_2} - {y_1})}^2}} $
Where $\left( {{x_1},{x_2}} \right)$ and $\left( {{y_1},{y_2}} \right)$ be the two points.
Area of the square $ = $ $side \times side$ unit sq.

Complete step-by-step answer:
Given points are $A = (3,4)$, $B = ( - 2,4)$, and $C = ( - 2, - 1)$
By plotting the points into graph we get,

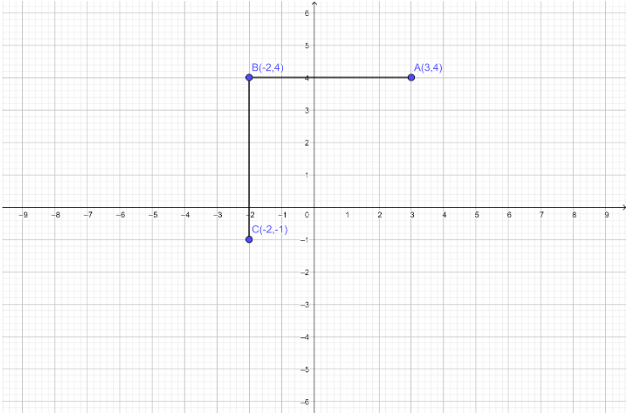
First we have to find the fourth vertex $D$ and the area of the given square $ABCD$.
In the square $ABCD$, we know all the sides are equal thus, the distance of each of the vertices are same
Hence we can write,
$AB = BC = CD = DA$
The points plotted on the graph below.
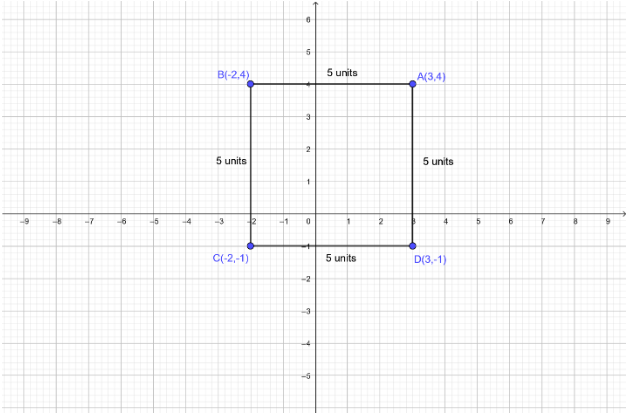
From the graph, the coordinates of point $D$ are $(3, - 1)$
Hence,

Now using the distance formula $D = \sqrt {{{({x_2} - {x_1})}^2} + {{({y_2} - {y_1})}^2}} ......(1)$
Using equation $(1)$ we can find out the side $AB$, so it will be
Here, $A = (3,4)$ where ${x_1} = 3,{y_1} = 4$ and $B = ( - 2,4)$ where ${x_2} = - 2,{y_2} = 4$
$\Rightarrow$$AB = \sqrt {{{( - 2 - 3)}^2} + {{(4 - 4)}^2}} $ $ = \sqrt {{{( - 5)}^2} + {0^2}} $$ = \sqrt {( - 5)( - 5) + 0} $$ = \sqrt {25} $$ = 5$ Units
Here,
$B = ( - 2,4)$ where ${x_1} = - 2$, ${y_1} = 4$ and
$C = ( - 2, - 1)$ where ${x_2} = - 2,{y_2} = - 1$
$\Rightarrow$$BC = \sqrt {{{( - 2 - ( - 2))}^2} + {{( - 1 - 4)}^2}} $$ = \sqrt {0 + {{( - 5)}^2}} = \sqrt {25} = 5$ Units
Now,
$C = ( - 2, - 1)$ where ${x_1} = - 2,{y_1} = - 1$ and
$D = (3, - 1)$ where ${x_2} = 3,{y_2} = - 1$
$\Rightarrow$$CD = \sqrt {{{(3 - ( - 2))}^2} + {{( - 1 - ( - 1))}^2}} = \sqrt {{5^2} + {0^2}} $$ = \sqrt {25} = 5$ Units
Now,
$D = (3, - 1)$where ${x_1} = 3,{y_1} = - 1$ and
$A = (3,4)$where ${x_2} = 3,{y_2} = 4$
$\Rightarrow$$DA = \sqrt {{{(3 - 3)}^2} + {{( - 1 - 4)}^2}} = \sqrt {{0^2} + {{( - 5)}^2}} = \sqrt {25} = 5$ Units
$D$ are $(3, - 1)$
Here we got the side $AB = 5$ unit sq.
Area of the square $ = $ side ×side
Area of the square $ABCD = AB \times AB$
Substituting the side value,
$ \Rightarrow 5 \times 5$
Multiplying both the numbers, we get
Hence,
Area of the square \[ABCD = 25\] Unit sq.

$\therefore $ The area of the square is $25$ unit sq.

Note: Whenever we face such types of problems the key behind the solution lies in the diagrammatic representation of the data provided then awareness about the basic formula can help in getting to the right track to reach the answer.