Question

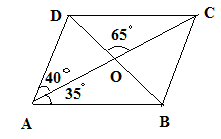
In the adjoining figure $ABCD$ is a parallelogram in which $\angle CAD = 40^\circ $, $\angle BAC = 35^\circ $ and $\angle COD = 65^\circ $. Calculate
A) $\angle ABD$
B) $\angle BDC$
C) $\angle CBD$

Answer 1

Hint: In this question, we have to calculate the value of the required angle. They give some angle values of the given parallelogram. By using those values into the facts that the opposite angles of a parallelogram are equal and the sum of the adjacent angles is $180^\circ $. We will get the required value of the angles.

Complete step-by-step answer:
Given In the given parallelogram $ABCD$, in which $\angle CAD = 40^\circ ,\angle BAC = 35^\circ $ and $\angle COD = 65^\circ $
We have to find the values of angles $\angle ABD$, $\angle BDC$, $\angle CBD$
Now we are finding one by one
Starting with the first one i) $\angle ABD$
It is given that the $\angle COD = 65^\circ $
So, $\angle COD = \angle AOB = 65^\circ $ (by using property -Vertical opposite angle)
And $\angle BAC$= $35^\circ $(given in the question)
We can say by using angle sum property
Here we get,
Therefore, $\angle BAC + \angle AOC + \angle ABO = 180^\circ $
(By using the concept -Sum of angle of triangle is $180^\circ $)
Let us put the values of the some known angles
$35^\circ + 65^\circ + \angle ABO = 180^\circ $
Angle sum of $\vartriangle OAB$
Hence, $\angle ABO = 80^\circ $
$\angle ABD = 80^\circ $
Now we proceed to the next part ii) $\angle BDC$
Now $AB\parallel CD$ $ABD$ and $BD$ is transversal lines
 $\angle ABD = \angle BDC$ ($\because $Alternate angles)
Hence we get, $\angle BDC = 80^\circ $
Now move to the next part that is (iii) $\angle CBD$
$\angle AOB + \angle BOC = 180^\circ $ ($\because $Linear pair)
We put the value of $\angle AOB = 65^\circ $, we get
$65^\circ + \angle BOC = 180^\circ $
$\angle BOC = 180^\circ - 65^\circ $
By doing subtraction, we have
$\angle BOC = 115^\circ $
$\angle DAO = \angle OCB$ (Alternate angles)
$\therefore \angle OCB = 40^\circ $
In $\vartriangle OCB$
$ \Rightarrow \angle BOC + \angle OCB + \angle CBO = 180^\circ $ (By using angle sum property of triangle)
Let us put the values of the known angles, we have
$ \Rightarrow 115^\circ + 40^\circ + \angle CBO = 180^\circ $
By adding the angles, we have
$ \Rightarrow 155^\circ + \angle CBD = 180^\circ $
$ \Rightarrow \angle CBD = 180^\circ - 155^\circ $
Now did subtraction on the right hand sided terms
We get,
$ \Rightarrow \angle CBD = 25^\circ $
Thus, $\angle CBD = 25^\circ $

Note: In these types of questions we need to know the properties of parallelogram Since opposite angles of a parallelogram are equal and adjacent angles of a parallelogram sum up to $180^\circ $. We can conclude all the angles of the parallelogram which we required in the question.