
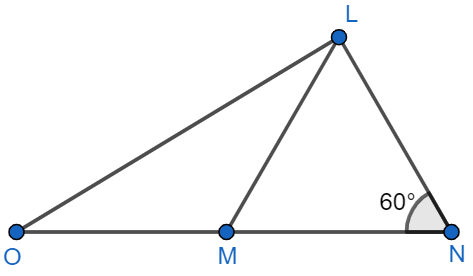
In the adjoining figure, \[LM\text{ }=\text{ }MO\] and \[LN\text{ }=\text{ }NM\]. Find: a) $\angle NLM$ b) $\angle LOM$.

Answer
598.2k+ views
Hint: We will use a concept that the angle opposite to the equal sides of the triangles are of equal measurement. For example, if ABC is a triangle, with $AB=AC$ then we can say that $\angle ABC=\angle ACB$. We will also use the angle sum property of triangles which state that the sum of all the angles of the triangle is equal to 180.
Complete step-by-step answer:
It is given in the question that $LM=MO$ and $LN=NM$ then we will have to find the angles $\angle NLM$ and $\angle LOM$.
We know that sum of all angles of a triangle is equal to 180 degree, so, in $\Delta LNM$, we have $\angle MNL+\angle NLM+\angle LMN={{180}^{{}^\circ }}.....(i)$.
We also know that angles opposite to the sides of equal length are of equal measurement value. In $\Delta LMN$, we have side \[LN\text{ }=\text{ }NM\], so from this, we can say that $\angle NLM=\angle LMN$.
On putting these value in the equation $\angle MNL+\angle NLM+\angle LMN={{180}^{{}^\circ }}.....(i)$ we get,
${{60}^{{}^\circ }}+\angle NLM+\angle NLM={{180}^{{}^\circ }}$, solving further, we get,
$2\angle NLM={{180}^{{}^\circ }}-{{60}^{{}^\circ }}$, therefore, we get finally,
\[\angle NLM=\dfrac{{{120}^{{}^\circ }}}{2}={{60}^{{}^\circ }}\].
Also, we get $\angle NML={{60}^{{}^\circ }}$.
We know that sum of linear pairs is equal to 180, and angles $\angle LMO\text{ }and\text{ }\angle LMN$ are forming linear pair, therefore,
$\angle LMO+\angle LMN={{180}^{{}^\circ }}$, putting the value $\angle NML={{60}^{{}^\circ }}$, we get,
$\angle LMO+{{60}^{{}^\circ }}={{180}^{{}^\circ }}$, therefore,
$\angle LMO={{180}^{{}^\circ }}-{{60}^{{}^\circ }}={{120}^{{}^\circ }}$.
Now, in $\Delta LMO$, we have sum of all three angles of the triangle as 180, it means $\angle LOM+\angle OML+\angle MLO={{180}^{{}^\circ }}$. Also, $\angle LOM=\angle MLO$ as they are angles opposite to equal sides, therefore we get,
$\angle LOM+{{120}^{{}^\circ }}+\angle LOM={{180}^{{}^\circ }}$, solving further, we get
$2\angle LOM={{180}^{{}^\circ }}-{{120}^{{}^\circ }}={{60}^{{}^\circ }}$, therefore, we finally get,
$\angle LOM=\dfrac{{{60}^{{}^\circ }}}{2}={{30}^{{}^\circ }}$.
Thus we get \[\angle NLM={{60}^{{}^\circ }}\] and $\angle LOM={{30}^{{}^\circ }}$.
Note: Usually students do miss-calculation in adding the angles of the triangle and it is enough to waste our all effort to solve this question. Generally, these silly mistakes are not traced even while revision, thus it is recommended to do calculation steps without mistakes. Sometimes students might think that triangle LMN is an equilateral triangle just by looking at it and then compute the angle, but it is not necessarily true always.
Complete step-by-step answer:
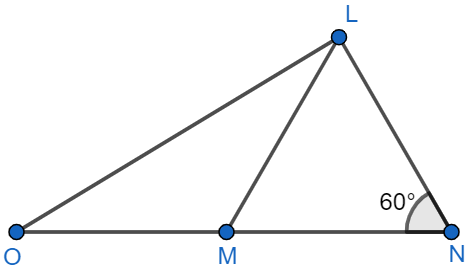
It is given in the question that $LM=MO$ and $LN=NM$ then we will have to find the angles $\angle NLM$ and $\angle LOM$.

We know that sum of all angles of a triangle is equal to 180 degree, so, in $\Delta LNM$, we have $\angle MNL+\angle NLM+\angle LMN={{180}^{{}^\circ }}.....(i)$.
We also know that angles opposite to the sides of equal length are of equal measurement value. In $\Delta LMN$, we have side \[LN\text{ }=\text{ }NM\], so from this, we can say that $\angle NLM=\angle LMN$.
On putting these value in the equation $\angle MNL+\angle NLM+\angle LMN={{180}^{{}^\circ }}.....(i)$ we get,
${{60}^{{}^\circ }}+\angle NLM+\angle NLM={{180}^{{}^\circ }}$, solving further, we get,
$2\angle NLM={{180}^{{}^\circ }}-{{60}^{{}^\circ }}$, therefore, we get finally,
\[\angle NLM=\dfrac{{{120}^{{}^\circ }}}{2}={{60}^{{}^\circ }}\].
Also, we get $\angle NML={{60}^{{}^\circ }}$.
We know that sum of linear pairs is equal to 180, and angles $\angle LMO\text{ }and\text{ }\angle LMN$ are forming linear pair, therefore,
$\angle LMO+\angle LMN={{180}^{{}^\circ }}$, putting the value $\angle NML={{60}^{{}^\circ }}$, we get,
$\angle LMO+{{60}^{{}^\circ }}={{180}^{{}^\circ }}$, therefore,
$\angle LMO={{180}^{{}^\circ }}-{{60}^{{}^\circ }}={{120}^{{}^\circ }}$.
Now, in $\Delta LMO$, we have sum of all three angles of the triangle as 180, it means $\angle LOM+\angle OML+\angle MLO={{180}^{{}^\circ }}$. Also, $\angle LOM=\angle MLO$ as they are angles opposite to equal sides, therefore we get,
$\angle LOM+{{120}^{{}^\circ }}+\angle LOM={{180}^{{}^\circ }}$, solving further, we get
$2\angle LOM={{180}^{{}^\circ }}-{{120}^{{}^\circ }}={{60}^{{}^\circ }}$, therefore, we finally get,
$\angle LOM=\dfrac{{{60}^{{}^\circ }}}{2}={{30}^{{}^\circ }}$.
Thus we get \[\angle NLM={{60}^{{}^\circ }}\] and $\angle LOM={{30}^{{}^\circ }}$.
Note: Usually students do miss-calculation in adding the angles of the triangle and it is enough to waste our all effort to solve this question. Generally, these silly mistakes are not traced even while revision, thus it is recommended to do calculation steps without mistakes. Sometimes students might think that triangle LMN is an equilateral triangle just by looking at it and then compute the angle, but it is not necessarily true always.
Recently Updated Pages
Two men on either side of the cliff 90m height observe class 10 maths CBSE

Cutting of the Chinese melon means A The business and class 10 social science CBSE

Show an aquatic food chain using the following organisms class 10 biology CBSE

How is gypsum formed class 10 chemistry CBSE

If the line 3x + 4y 24 0 intersects the xaxis at t-class-10-maths-CBSE

Sugar present in DNA is A Heptose B Hexone C Tetrose class 10 biology CBSE

Trending doubts
Why is there a time difference of about 5 hours between class 10 social science CBSE

What is the median of the first 10 natural numbers class 10 maths CBSE

Indias first jute mill was established in 1854 in A class 10 social science CBSE

Indias first jute mill was established in 1854 in A class 10 social science CBSE

Write a letter to the principal requesting him to grant class 10 english CBSE

The Equation xxx + 2 is Satisfied when x is Equal to Class 10 Maths




