Question

In the Cartesian plane, $O$ is the origin of the coordinate axes. A person starts at $O$ and walks a distance of $3{\text{ units}}$ in the NORTH-EAST direction and reaches the point $P$ . From $P$ , he walks ${\text{4 units}}$ of distance parallel to NORTH-WEST direction and reaches the point $Q$. Express the vector $\mathop {OQ}\limits^ \to $ in terms of $\vec i$ and $\vec j$ $\left( {Observe{\text{ }}\angle {\text{XOP = 4}}{{\text{5}}^ \circ }} \right)$.

Answer 1

Hint: In this question, first of all, we will find the projection of the point $P$ on $x - axis$ , and $y - axis$ then with this, we will get the point $P$ position. Similarly, we will find the coordinate for $Q$ , and then finally we will get $\mathop {OQ}\limits^ \to $ by position vector of $Q$ minus the position vector of $O$.

Complete step-by-step answer:
Since a person walks the distance of $3{\text{ units}}$ in the NORTH-EAST

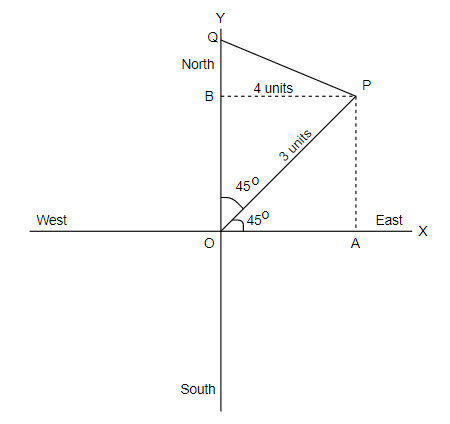
Therefore, the projection of the point $P$on $x - axis$and $y - axis$ will be
$ \Rightarrow OP\cos {45^ \circ }$
Now on substituting the values, we get
$ \Rightarrow 3 \times \dfrac{1}{{\sqrt 2 }}$
And on solving, we get
$ \Rightarrow \dfrac{3}{{\sqrt 2 }}$
Similarly,
$ \Rightarrow OP\sin {45^ \circ }$
$ \Rightarrow 3 \times \dfrac{1}{{\sqrt 2 }}$
And on solving, we get
$ \Rightarrow \dfrac{3}{{\sqrt 2 }}$
Therefore, the point \[P = \left( {\dfrac{3}{{\sqrt 2 }},\dfrac{3}{{\sqrt 2 }}} \right)\]
Now since \[\angle {\text{POA = 4}}{{\text{5}}^ \circ }\]
And we know \[\angle {\text{POA = }}\angle BPO\] , because on the opposite sides alternate angles are equal.
Therefore, \[\angle BPO{\text{ = 4}}{{\text{5}}^ \circ }\]
Now if \[\angle BPO{\text{ = 4}}{{\text{5}}^ \circ }\]
Then,\[\angle QPB{\text{ = 9}}{{\text{0}}^ \circ }{\text{ - 4}}{{\text{5}}^ \circ } = {45^ \circ }\] since the sum of the right angles be${90^ \circ }$.
Now again at the point $P$
$BP = 4\cos {45^ \circ }$
And on substituting the values, we get
$ \Rightarrow 4 \times \dfrac{1}{{\sqrt 2 }}$
On solving the above equation, we get
$ \Rightarrow \dfrac{4}{{\sqrt 2 }}$
Similarly, for $QB$
$BP = 4\sin {45^ \circ }$
And on substituting the values, we get
$ \Rightarrow 4 \times \dfrac{1}{{\sqrt 2 }}$
On solving the above equation, we get
$ \Rightarrow \dfrac{4}{{\sqrt 2 }}$
So, form the above the coordinate of $Q$ will be given as
$ \Rightarrow Q = \left[ { - \left( {\dfrac{4}{{\sqrt 2 }} - \dfrac{3}{{\sqrt 2 }}} \right),\left( {\dfrac{4}{{\sqrt 2 }} + \dfrac{3}{{\sqrt 2 }}} \right)} \right]$
And on solving, we get
$ \Rightarrow Q = \left( { - \dfrac{1}{{\sqrt 2 }},\dfrac{7}{{\sqrt 2 }}} \right)$
Therefore, $\mathop {OQ}\limits^ \to $ by position vector of $Q$ minus the position vector of $O$
So on substituting the values, we get
$ \Rightarrow \mathop {OQ}\limits^ \to = - \dfrac{1}{{\sqrt 2 }}\mathop i\limits^ \wedge + \dfrac{7}{{\sqrt 2 }}\mathop j\limits^ \wedge - 0\mathop i\limits^ \wedge - 0\mathop j\limits^ \wedge $
And on solving the above equation, we get
$\mathop { \Rightarrow OQ}\limits^ \to = - \dfrac{1}{{\sqrt 2 }}\mathop i\limits^ \wedge + \dfrac{7}{{\sqrt 2 }}\mathop j\limits^ \wedge $
Therefore the vector in terms $\mathop i\limits^ \wedge {\text{ and }}\mathop j\limits^ \wedge $ will be $ - \dfrac{1}{{\sqrt 2 }}\mathop i\limits^ \wedge + \dfrac{7}{{\sqrt 2 }}\mathop j\limits^ \wedge $

Note: The important point to note in this question is we should always draw the figure before solving it as it will reduce the complexity and help to understand it better. And also while solving we have to be aware of the signs and calculations. By using the simple geometry theorems we can easily solve this problem.