Question

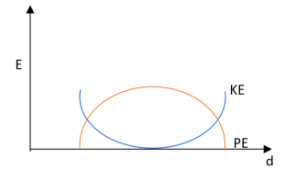
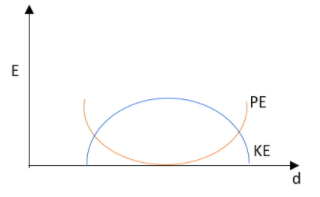
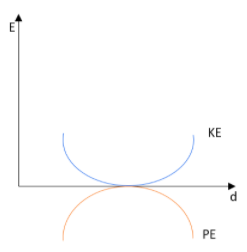
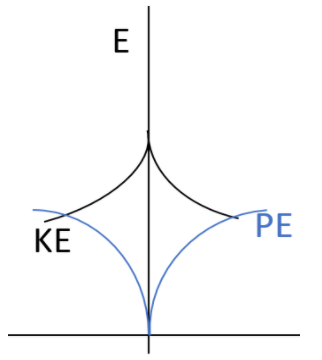
in the case of a simple pendulum, a graph has been represented between its kinetic energy, KE and its potential energy, PE against displacement $d$. Identify which one of the following is best representing these correctly? (Graph is schematic and not drawn to scale)
A.

B.

C.

D.

Answer 1

Hint: The kinetic energy in a simple harmonic motion can be found by taking the half of the product of the mass and square of the velocity. Using this find out the variation in potential energy and kinetic energy with a displacement. This will help you in answering this question.

Complete answer:
The kinetic energy in a simple harmonic motion can be found by taking the half of the product of the mass and square of the velocity. That is we can write that,
$KE=\dfrac{1}{2}m{{u}^{2}}$
Where $u$ be the velocity. The velocity of the simple pendulum in a SHM can be shown as,
$u=\sqrt{\left( {{A}^{2}}-{{x}^{2}} \right){{\omega }^{2}}}$
Substituting this in the equation of kinetic energy will give,
\[KE=\dfrac{1}{2}m\left( {{A}^{2}}-{{x}^{2}} \right){{\omega }^{2}}\]
As we all know the spring constant can be found as,
\[K=m{{\omega }^{2}}\]
Substituting this value in the equation will give,
\[KE=\dfrac{1}{2}K\left( {{A}^{2}}-{{x}^{2}} \right)\]
For a simple pendulum, the variation in kinetic energy and potential energy with displacement \[d\] will be,
\[\begin{align}
  & KE=\dfrac{1}{2}m{{\omega }^{2}}\left( {{A}^{2}}-{{d}^{2}} \right) \\
 & PE=\dfrac{1}{2}m{{\omega }^{2}}{{d}^{2}} \\
\end{align}\]
If the displacement is zero, then,
\[\begin{align}
  & KE=\dfrac{1}{2}m{{\omega }^{2}}{{A}^{2}} \\
 & PE=0 \\
\end{align}\]
If the displacement be,
\[d=\pm A\]
Then we can write that,
\[\begin{align}
  & PE=\dfrac{1}{2}m{{\omega }^{2}}{{A}^{2}} \\
 & KE=0 \\
\end{align}\]
Using these relations, we can plot the graph. That is the graph will look like this,

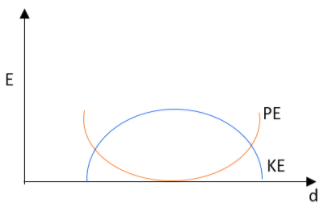
Therefore the correct answer has been obtained as option B.

Note:
The potential energy of a system is defined as the energy acquired by the system because of its orientation and position in the space. The kinetic energy of a system is defined as the energy possessed by a body because of the motion of the system. Both of them are having the same units of energy.