Question

In the circuit shown initially \[{C_1}\] and ${C_2}$ are uncharged, after closing the circuit

A) the charge on ${C_2}$ is greater than the charge on ${C_1}$.
B) charge on ${C_1}$ and ${C_2}$ are the same.
C) the potential drops across both the capacitors are the same.
D) the potential drop across ${C_2}$ is greater than that across ${C_1}$.

Answer 1

Hint: In series combination for capacitors the charge on each capacitor is the same. The total voltage in a series combination for voltage source is the sum of individual voltages. On closing the switch the capacitors begin to charge and then acquire equilibrium state.

Complete step by step answer:
A capacitor is an electrically passive device that is used to store electrical energy.
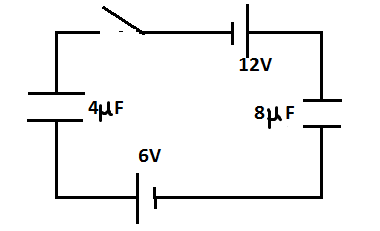
In the given circuit, the voltage sources are in series. Hence, the equivalent voltage for the circuit will be the sum of the individual voltages.
Hence, ${V_{total}} = {V_1} + {V_2}$ -------🡪 (here, ${V_{total}}$ is the equivalent voltage for the circuit)
For the given circuit, ${V_1},{V_2}$ are 12V and 6V respectively.
Thus, equivalent voltage= ${V_{total}} = 12 + 6 = 18V$-------- 🡪(equation 1)
Also, the capacitors ${C_1}$ and ${C_2}$ are in series, hence, equivalent capacitance of the circuit is given by;
$\dfrac{1}{{{C_{eq}}}} = \dfrac{1}{{{C_1}}} + \dfrac{1}{{{C_2}}}$ -------------🡪 (series combination of capacitors)
And, ${C_1} = 4\mu F$, ${C_2} = 8\mu F$----------🡪 (given)
Hence,
$\Rightarrow \dfrac{1}{{{C_{eq}}}} = \dfrac{1}{4} + \dfrac{1}{8}$ ------- 🡪(substituting the values in the formula)
$ = \dfrac{{8 + 4}}{{32}}$
Thus, ${C_{eq}} = \dfrac{{32}}{{12}}$
$\Rightarrow {C_{eq}} = \dfrac{8}{3}$--------------🡪 (equation 2)
Also, we know that, the charge stored in a capacitor is given by,
$Q = CV$-------------- 🡪(here, C is the capacitance, V is the voltage)
Thus, ${Q_{eq}} = {C_{eq}} \times {V_{total}}$
$\Rightarrow {Q_{eq}} = \dfrac{8}{3} \times 18 = 8 \times 6$
Hence,${Q_{eq}} = 48\mu C$.
Also, the capacitors are in series, so the charge in each capacitor is the same.
Thus, ${Q_{eq}} = {Q_1} = {Q_2}$ ---------- 🡪(property of capacitors in series)
Hence, voltage across ${C_1}$ is ${V_1} = \dfrac{{{Q_1}}}{{{C_1}}}$------- 🡪(here, ${Q_1} = {Q_{eq}}$ and ${C_1} = 4\mu F$)
$\Rightarrow {V_1} = \dfrac{{48}}{4} = 12V$
Similarly for voltage across${C_2}$, ${V_2} = \dfrac{{{Q_2}}}{{{C_2}}}$ --------- 🡪(here, ${Q_2} = {Q_{eq}}$ and ${C_2} = 8\mu F$)
$\Rightarrow {V_2} = \dfrac{{48}}{8} = 6V$

Hence, the two capacitors have the same charge. Therefore, option B is correct.

Note:
In series combination the voltage across individual elements is different but the current is the same, hence, the charge is the same.
In parallel combination, the voltage is the same across all elements but the current is different and so is the charge.
Equivalent capacitance for series =$\dfrac{1}{{{C_{eq}}}} = \dfrac{1}{{{C_1}}} + \dfrac{1}{{{C_2}}} + \dfrac{1}{{{C_3}}} + ............$
Equivalent capacitance for parallel = ${C_{eq}} = {C_1} + {C_2} + {C_3} + ............$