
In the experiment on the photoelectric effect, the graph between \[\mathop E\nolimits_K (\max )\] and \[\nu \] is found to be a straight line as shown in fig. The threshold frequency and Planck's constant according to this graph are:
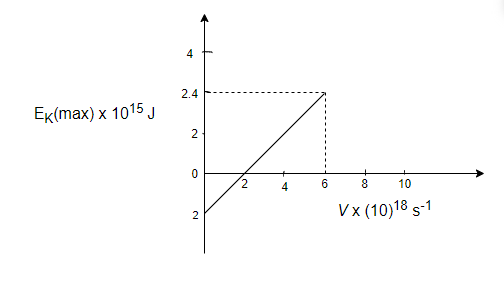
A) \[3.33 \times \mathop {10}\nolimits^{18} \]$s^{-1}$, \[6 \times \mathop {10}\nolimits^{ - 34} \]J-s
B) \[6 \times \mathop {10}\nolimits^{18} \] $s^{-1}$, \[6 \times \mathop {10}\nolimits^{ - 34} \] J-s
C) \[2.66 \times \mathop {10}\nolimits^{18} \] $s^{-1}$, \[4 \times \mathop {10}\nolimits^{ - 34} \] J-s
D) \[4 \times \mathop {10}\nolimits^{18} \] $s^{-1}$, \[3 \times \mathop {10}\nolimits^{ - 34} \] J-s
Answer
121.5k+ views
Hint: This given problem can be solved by Einstein’s photoelectric equation. Einstein explained the various laws of photoelectric emission on the basis of Planck’s quantum theory. According to Planck’s quantum theory, the energy of a photon is given by \[E = h\nu \].
Complete step by step solution:
Step 1:
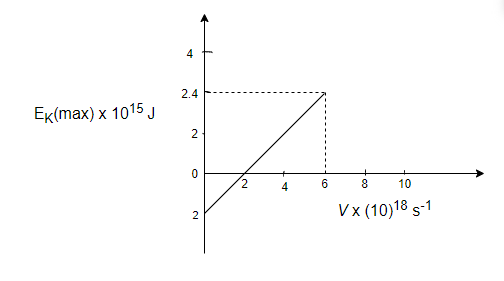
Einstein assumed that one photoelectron is ejected from a metal surface if one photon of suitable light radiation falls on it.
Let us consider a photon of light of frequency \[\nu \], incident on a photosensitive metal surface. The energy of the photon is \[h\nu \], spent in two ways:
A part of the energy of the photon will be used in liberating the electron from the metal surface which is equal to the work function \[\mathop \phi \nolimits_0 \] of the metal.
The rest of the energy of the photon will be used in imparting the maximum kinetic energy \[\mathop K\nolimits_{\max } \] to the emitted photoelectron.
So, from above two points, we will get-
\[h\nu = \mathop \phi \nolimits_0 + \mathop K\nolimits_{\max } \].................(1)
This equation (1) is known as Einstein’s photoelectric equation.
Step 2: Now from the equation (1) –
\[h\nu = \mathop \phi \nolimits_0 + \mathop K\nolimits_{\max } \]; where \[\mathop \phi \nolimits_0 = \]work function of metal, \[h = \]Planck’s constant, and \[\nu = \]frequency of incident photon
If we rearrange the equation (1) in the form of \[\mathop K\nolimits_{\max } = h\nu + \mathop \phi \nolimits_0 \] and this equation can be compared with the \[y = mx + c\] .
So, the slope of the given line will be \[h\] and the intercept will be \[ - \mathop \phi \nolimits_0 \].
So, from the graph, \[h = \dfrac{{\mathop K\nolimits_{\max } }}{{\mathop \nu \nolimits_2 - \mathop \nu \nolimits_1 }}\]
\[h = \dfrac{{2.4 \times \mathop {10}\nolimits^{ - 15} }}{{\left( {6 - 2} \right) \times \mathop {10}\nolimits^{18} }}\]
\[h = 6 \times \mathop {10}\nolimits^{ - 34} \]J-s
And \[\mathop \phi \nolimits_0 = 2 \times \mathop {10}\nolimits^{ - 15} \]J
\[\mathop \phi \nolimits_0 = h\mathop \nu \nolimits_0 \]; where \[\mathop \nu \nolimits_0 = \] threshold frequency
\[\mathop \nu \nolimits_0 = \dfrac{{\mathop \phi \nolimits_0 }}{h} = \dfrac{{2 \times \mathop {10}\nolimits^{ - 15} }}{{6 \times \mathop {10}\nolimits^{ - 34} }}\]
\[\mathop \nu \nolimits_0 = 3.33 \times \mathop {10}\nolimits^{18} \]$s^{-1}$
So, the correct option is (A).
Note: If \[\nu < \mathop \nu \nolimits_0 \] , then maximum K.E. will be negative, which is not possible. So, Photoelectric emission does not occur if the frequency of incident radiation is less than the threshold frequency.
Complete step by step solution:
Step 1:
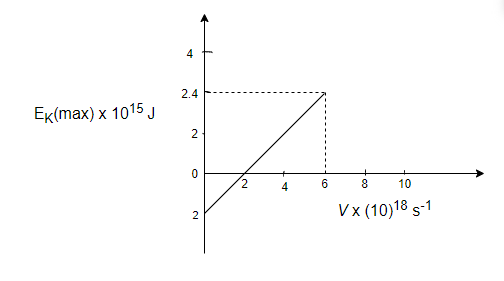
Einstein assumed that one photoelectron is ejected from a metal surface if one photon of suitable light radiation falls on it.
Let us consider a photon of light of frequency \[\nu \], incident on a photosensitive metal surface. The energy of the photon is \[h\nu \], spent in two ways:
A part of the energy of the photon will be used in liberating the electron from the metal surface which is equal to the work function \[\mathop \phi \nolimits_0 \] of the metal.
The rest of the energy of the photon will be used in imparting the maximum kinetic energy \[\mathop K\nolimits_{\max } \] to the emitted photoelectron.
So, from above two points, we will get-
\[h\nu = \mathop \phi \nolimits_0 + \mathop K\nolimits_{\max } \].................(1)
This equation (1) is known as Einstein’s photoelectric equation.
Step 2: Now from the equation (1) –
\[h\nu = \mathop \phi \nolimits_0 + \mathop K\nolimits_{\max } \]; where \[\mathop \phi \nolimits_0 = \]work function of metal, \[h = \]Planck’s constant, and \[\nu = \]frequency of incident photon
If we rearrange the equation (1) in the form of \[\mathop K\nolimits_{\max } = h\nu + \mathop \phi \nolimits_0 \] and this equation can be compared with the \[y = mx + c\] .
So, the slope of the given line will be \[h\] and the intercept will be \[ - \mathop \phi \nolimits_0 \].
So, from the graph, \[h = \dfrac{{\mathop K\nolimits_{\max } }}{{\mathop \nu \nolimits_2 - \mathop \nu \nolimits_1 }}\]
\[h = \dfrac{{2.4 \times \mathop {10}\nolimits^{ - 15} }}{{\left( {6 - 2} \right) \times \mathop {10}\nolimits^{18} }}\]
\[h = 6 \times \mathop {10}\nolimits^{ - 34} \]J-s
And \[\mathop \phi \nolimits_0 = 2 \times \mathop {10}\nolimits^{ - 15} \]J
\[\mathop \phi \nolimits_0 = h\mathop \nu \nolimits_0 \]; where \[\mathop \nu \nolimits_0 = \] threshold frequency
\[\mathop \nu \nolimits_0 = \dfrac{{\mathop \phi \nolimits_0 }}{h} = \dfrac{{2 \times \mathop {10}\nolimits^{ - 15} }}{{6 \times \mathop {10}\nolimits^{ - 34} }}\]
\[\mathop \nu \nolimits_0 = 3.33 \times \mathop {10}\nolimits^{18} \]$s^{-1}$
So, the correct option is (A).
Note: If \[\nu < \mathop \nu \nolimits_0 \] , then maximum K.E. will be negative, which is not possible. So, Photoelectric emission does not occur if the frequency of incident radiation is less than the threshold frequency.
Recently Updated Pages
Young's Double Slit Experiment Step by Step Derivation

Difference Between Circuit Switching and Packet Switching

Difference Between Mass and Weight

JEE Main Participating Colleges 2024 - A Complete List of Top Colleges

Sign up for JEE Main 2025 Live Classes - Vedantu

JEE Main 2025 Helpline Numbers - Center Contact, Phone Number, Address

Trending doubts
JEE Main Login 2045: Step-by-Step Instructions and Details

JEE Main Chemistry Exam Pattern 2025

Charging and Discharging of Capacitor

Collision - Important Concepts and Tips for JEE

JEE Mains 2025 Correction Window Date (Out) – Check Procedure and Fees Here!

Clemmenson and Wolff Kishner Reductions for JEE

Other Pages
JEE Advanced 2025: Dates, Registration, Syllabus, Eligibility Criteria and More

JEE Main 2022 June 25 Shift 2 Question Paper with Answer Keys & Solutions

JEE Main Maths Paper Pattern 2025

Electromagnetic Waves Chapter - Physics JEE Main

JEE Advanced 2025 Revision Notes for Practical Organic Chemistry

JEE Advanced 2025 Revision Notes for Physics on Modern Physics




