Question

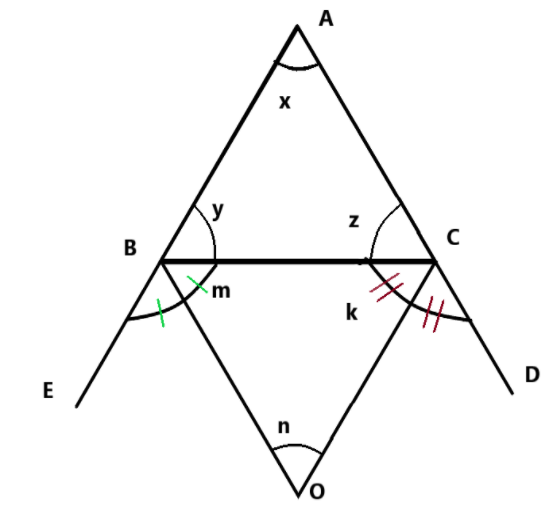
In the fig. sides AB and AC of triangle ABC are produced to point E and D respectively . if bisectors BO and CO of \[\angle CBE\;\] and \[\angle BCD\] respectively meet at point O, then prove that \[\angle BOC = 90^\circ - \dfrac{1}{2}\angle BAC.\]

Answer 1

Hint: The sum of all angles of triangles is 180. Also, the angle of a straight line is 180. A line that divides an angle into two equal halves is known as an angle bisector. An angle bisector exists for every angle. It's also the symmetry line that connects an angle's two arms.

Complete step-by-step solution:
We have given that the triangle ABC has extended arms and OB and OC are the angle bisectors of \[\angle OBE\] and \[\angle OCD\] respectively.
We also assume \[\angle OBC = m\] , \[\angle OCB = k\] and \[\angle BOC = n\] .
And we have to prove \[n = 90^\circ - \dfrac{1}{2}\angle BAC\].
We have given triangle ABC so,
Sum of all angles of triangle =180
X+Y+Z=180 (1)
We will divide the equation by 2 to get the value of \[\dfrac{X}{2}\]
\[\dfrac{{X + Y + Z}}{2} = 90\]
\[\Rightarrow \dfrac{X}{2} = 90 - \dfrac{y}{2} - \dfrac{z}{2}\]
We also know that angle of a straight line is 180, so
\[\angle EBC + \angle CBA = 180\]
\[\angle EBC = 180 - \angle CBA\]
Since OB is bisector
We will divide the \[\angle EBC\] by 2 to get \[\angle OBC\]
\[\angle OBC = 90 - \dfrac{{\angle CBA}}{2}\]
\[\Rightarrow m = 90 - \dfrac{{\angle CBA}}{2}\]
\[\Rightarrow m = 90 - \dfrac{y}{2}\]\[\]
Similarly, \[\angle BCO = 90 - \dfrac{{\angle BCA}}{2}\]
\[k = 90 - \dfrac{{\angle BCA}}{2}\]
\[k = 90 - \dfrac{z}{2}\]
Now , in triangle BOC we have
\[m + n + k = 180\]
We have substituted the value of m and n in above equation,
\[90 - \dfrac{y}{2} +n+ 90 - \dfrac{z}{2} = 180\]
We have rearranged it
\[90 + 90 - \dfrac{y}{2} - \dfrac{z}{2} + n = 180\]
Then we substituted the value as we know that \[\dfrac{X}{2} = 90 - \dfrac{y}{2} - \dfrac{z}{2}\]
\[90 + \dfrac{X}{2} + n = 180\]
\[\Rightarrow n = 90 - \dfrac{X}{2}\]
So , we have proved that \[\angle BOC = 90^\circ - \dfrac{1}{2}\angle BAC.\]
where \[\dfrac{X}{2} = \angle BAC\] and \[n = \angle BOC\].

Note: We have to take care about how we can convert the given value in our desired result. Sometimes we are so close to the answer but can't write in the given format. We should be good at the different theorems and properties of triangles. Figure is also a very important part for these types of questions.