Question

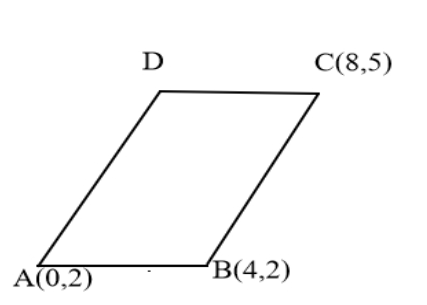
In the figure, ABCD is a parallelogram.
a) Write the coordinates of D.
b) What is the height of this parallelogram?
c) Find the perimeter and area of it.

Answer 1

Hint: Here we will find the coordinates of D, height, perimeter and area of the parallelogram by considering the geometry concepts and properties of parallelogram.

Complete step-by-step answer:
a) Coordinates of D
Distance between A and B
$ \Rightarrow \sqrt {{{(4 - 0)}^2} + {{(2 - 2)}^2}} = \sqrt {16} = 4$
Since the opposite sides of a parallelogram are equal, the distance between C and D is also 4. Also, the y-coordinates of A and B are equal, the sides AB is parallel to the x-axis. And since ABCD is a parallelogram, CD is also parallel to the x-axis. So the y-coordinates of C and D are also equal.
Thus, the x-coordinate of $D = 8 - 4 = 4$
Hence, the coordinates of ’D’ are (4, 5).

b) Height of the parallelogram
The x-coordinates of D and B are equal. So the line BD is parallel to the y-axis or BD is perpendicular to the x-axis.
So, height of the parallelogram $ = DB = \left| {{y_1} - {y_2}} \right| = \left| {5 - 2} \right| = 3$

c) Perimeter and area of the parallelogram
Find the distance between B and C
$
BC = \sqrt {{{({x_2} - {x_1})}^2} + {{({y_2} - {y_1})}^2}} \\
BC = \sqrt {{{(8 - 4)}^2} + {{(5 - 2)}^2}} \\
BC = \sqrt {{{(4)}^2} + {{(3)}^2}} \\
BC = \sqrt {16 + 9} \\
BC = \sqrt {25} = 5 \\
$
$AD = BC = 5{\text{ units}}$


Perimeter=$2(4 + 5) = 2 \times 9 = 18$units.
Area=Base x Height
Area$ = 4 \times 3 = 12$ sq .units

Note: In this type of question we have to apply the relationship between the parallel line and perpendicular line and use the various formulas like distance formula to arrive at the solution.