Question

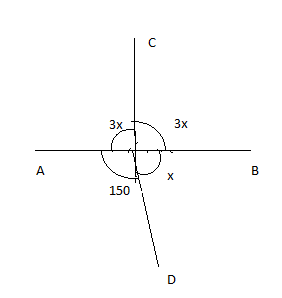
In the figure determine the value of x.

$A) 80_{}^\circ$
$B) 60_{}^\circ$
$C) 50_{}^\circ$
$D) 30_{}^\circ$

Answer 1

Hint: To solve this question we need to apply the concept that the total angle in a straight line equals to $180_{}^\circ$.

Complete step by step answer:
Since the total angle in a straight line equals to $180_{}^\circ$.
Now from the diagram,
We can write that the sum of $3x$ and $3x$ is equal to $180_{}^\circ$ and the sum of $\Rightarrow 150_{}^\circ$ and $x$ also equals to $180_{}^\circ$.
Therefore, $3x + 3x = 180_{}^\circ$
$\Rightarrow 6x = 180_{}^\circ$
On dividing the terms we get the value of $x$
So, $x = 30_{}^\circ$
Also, we can write
$\Rightarrow x + 150_{}^\circ = 180_{}^\circ$
By moving $150_{}^\circ$ on the right hand side we get-
$\Rightarrow x = 180_{}^\circ - 150_{}^\circ$
On subtracting the terms we get,
$\Rightarrow x= 30_{}^\circ$

So it is verified that in both the cases the value of x $ = 30_{}^\circ$ since the angles lie on the same straight line. Thus, the correct option is $D$.

Note:
- In mathematics, an angle whose vertex point has a value of 180 degrees is a straight angle. Essentially, it makes a straight line from the vertex, the sides of which lie in opposite directions. They are often referred to as "flat angles".
- A straight angle is exactly half of the revolution that is $360_{}^\circ$.
- A straight angle inverts the point’s path.
- By adding two right angles, a straight angle can be formed.
- By rotating one ray 180° with respect to another ray, a straight angle is created.
- Real-life examples of a straight angle include see-saw, the inclined plane of the staircase, plane surface, straight stick, etc.
- The positive straight angle, that is, $180_{}^\circ$ is a straight angle determined anti-clockwise.
- A negative straight angle, that is, $ - 180_{}^\circ$ is a straight angle determined clockwise.
- The arms extend in the reverse direction at a straight angle.