Question

In the figure, find the value of x for which the lines l and m are parallel.

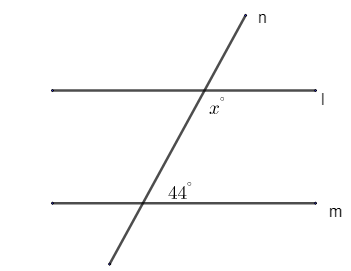
(a)\[{{136}^{\circ }}\]
(b)\[{{44}^{\circ }}\]
(c)\[{{46}^{\circ }}\]
(d)\[{{134}^{\circ }}\]

Answer 1

Hint: In the parallel lines use the concept of interior angles and apply the property that the sum of interior angles is \[{{180}^{\circ }}\], thus substitute the value and find the value of x.

Complete step-by-step answer:
In the question we are given a figure and we have to find the value of x.
The figure is,

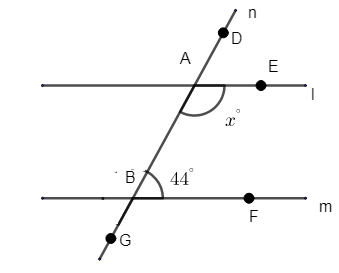
It contains two straight lines l, m which are parallel to each other which is cut by a straight line n or a transversal at two points let it be named as A, B.
So, here angle of A is measured as x and angle of B is given as B. As we know that here angle A and angle B together known as co – interior angles or we can say that if two parallel lines are cut by transversal like l and m by line n then \[\angle BAE\] and \[\angle ABF\] cuts as co – interior angles that it’s sum is equal to \[{{180}^{\circ }}\] or 2 right angles.
So, according to that,
\[\angle EAB+\angle ABF={{180}^{\circ }}\]
As we are given that \[\angle EAB\] is ‘x’ and \[\angle ABF={{44}^{\circ }}\]. So, on substituting we can write it as,
\[x+{{44}^{\circ }}={{180}^{\circ }}\]
Or, \[x={{180}^{\circ }}-{{44}^{\circ }}\]
So, the value of x is \[{{136}^{\circ }}\].
Hence, the correct option is (a).

Note: We can also use the concept of corresponding angles, that corresponding angles are equal. Hence, corresponding angles are \[\angle DAE\] and \[\angle ABF\] which are equal. After then apply angles in a straight line which sums up to \[{{180}^{\circ }}\].