Question

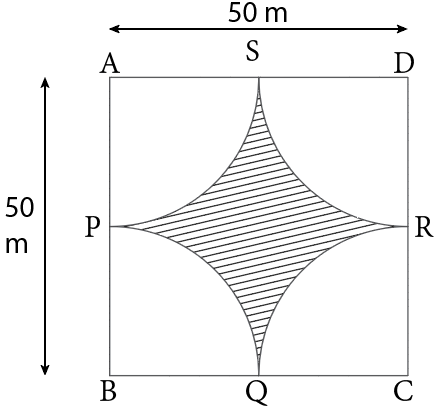
In the figure given here $\square ABCD$ is a square of side 50 m. Points P, Q, R and S are the mid-points of side AB, BC, CD and AD respectively. Find the area of the shaded region.

Answer 1

Hint: Firstly, find the area of square $\square ABCD$ .
Then, find radii of the given quarter circles and thus find the total area of the 4 quarter circles.
Finally, subtract the area of 4 quarter circles from the area of the square to get the area of the required shaded area.

Complete step-by-step answer:
Here, $\square ABCD$ is a square of side 50 m.
So the area of square $\square ABCD$ is $ABCD = {\left( {50} \right)^2} = 2500{m^2}$ .
Now, there are 4 quarter circles given in the diagram with centres of the circles as points A, B, C and D and also points P, Q, R and S are the mid-points of side AB, BC, CD and AD respectively.
Thus, the length of the segment AP = PB = BQ = QC = CR = RD = DS = SA $ = \dfrac{{50}}{2} = 25m$ .
So, the radii of the given quarter circles are 25 m each.
Now, the area of 4 quarter circles with radii 25 m each is given by $4 \times \dfrac{{\pi {r^2}}}{4} = \pi {r^2}$ .
Thus, the are of given 4 quarter circles $ = \pi {\left( {25} \right)^2}$
    $
 = \dfrac{{22}}{7} \times 625 \\
 = 1964.28 \\
 = 1964{m^2} \\
 $
Now, the area of the shaded part can be given by the difference of area of square and the area of 4 quarter circles.
$\therefore $ Area of shaded region $ = 2500 - 1964 = 536{m^2}$ .
Thus, we get the required area as $536{m^2}$ .

Note: Try to remember the following formula for solving these types of questions 1.Area of a square with length of side $a = {a^2}$
2.Area of a circle with radius $r = \pi {r^2}$
3.Area of semicircle with radius of circle $r = \dfrac{{\pi {r^2}}}{2}$
4.Area of quarter circle with radius of circle $r = \dfrac{{\pi {r^2}}}{4}$