
In the figure, if
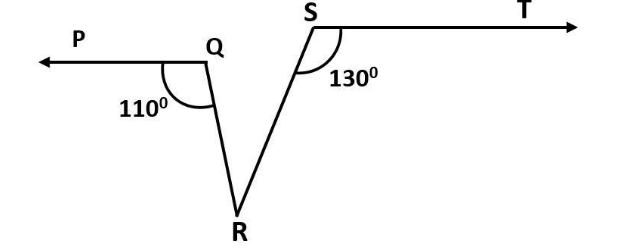

Answer
491.1k+ views
Hint: Draw a flat parallel line passing through point
Complete step-by-step answer:
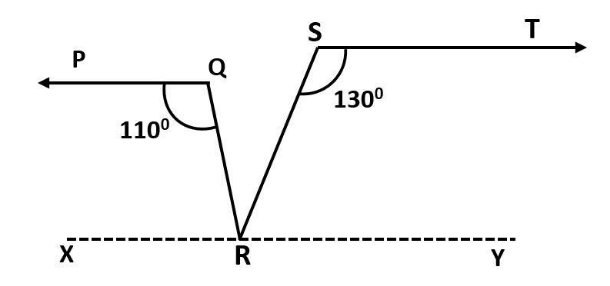
Observe the diagram
We have done a construction for the simplicity of the question.
Let us assume, XY is a line, passing through R in such a way that it is parallel to PQ and ST. i.e.
Now, since, parts of parallel lines are parallel, we can say that,
And, using the transverse line rule for the transverse QR, we can say that
It is given to us that,
By substituting this value in the above equation, we get
By rearranging it, we get
Again, by using the property that, the parts of parallel lines are parallel, we can say that,
And, using the transverse line rule for the transverse RS, we can say that
It is given to us that,
By substituting this value in the above equation, we get
By rearranging it, we get
Now, we know that, a straight line always makes and angle of
But,
Therefore, we can write
By substituting the values of
By re-arranging it, we get
Note: Sometimes, you need to understand that a construction is necessary to simplify the question. Like in this question, without the construction that we did, there would have been to ground to find a relationship between the given information and
Complete step-by-step answer:

Observe the diagram
We have done a construction for the simplicity of the question.
Let us assume, XY is a line, passing through R in such a way that it is parallel to PQ and ST. i.e.
Now, since, parts of parallel lines are parallel, we can say that,
And, using the transverse line rule for the transverse QR, we can say that
It is given to us that,
By substituting this value in the above equation, we get
By rearranging it, we get
Again, by using the property that, the parts of parallel lines are parallel, we can say that,
And, using the transverse line rule for the transverse RS, we can say that
It is given to us that,
By substituting this value in the above equation, we get
By rearranging it, we get
Now, we know that, a straight line always makes and angle of
But,
Therefore, we can write
By substituting the values of
By re-arranging it, we get
Note: Sometimes, you need to understand that a construction is necessary to simplify the question. Like in this question, without the construction that we did, there would have been to ground to find a relationship between the given information and
Recently Updated Pages
Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 Business Studies: Engaging Questions & Answers for Success

Master Class 11 Accountancy: Engaging Questions & Answers for Success

Questions & Answers - Ask your doubts

Master Class 11 Accountancy: Engaging Questions & Answers for Success

Master Class 11 Science: Engaging Questions & Answers for Success

Trending doubts
List some examples of Rabi and Kharif crops class 8 biology CBSE

What is the feminine gender of a stag class 8 english CBSE

Write five sentences about Earth class 8 biology CBSE

Summary of the poem Where the Mind is Without Fear class 8 english CBSE

How many ten lakhs are in one crore-class-8-maths-CBSE

Advantages and disadvantages of science




